I always advise students not to tie themselves to one piece of statistical software, even when it is as good as Stata. It is inevitable that whichever statistical package they choose, there will be tasks that are easier in another program or analyses that their favourite does not offer.
The problem with this advice is that it takes time to develop advanced skills in using statistical software and many people do not have the time or inclination to learn a second program.
The solution is to develop methods that enable us to work primarily in Stata, but to export jobs to other packages when necessary and then to read the results into Stata for further investigation. This is the method that we use for running Bayesian analyses by combining Stata and WinBUGS and I have discussed in past postings, how we can call R from Stata to take advantage of the many analyses available in R but not in Stata.
In an ideal world, Stata would make it automatic for you to export a job and to import the results but unfortunately it does not, perhaps for obvious economic reasons. None the less it is not difficult to implement such a scheme for ourselves.
R is organized in packages, which are collections of related programs and data. There is a particularly good package called MCMCglmm that fits Bayesian generalized linear mixed models and since there is nothing similar in Stata, a sensible option would be to send the Poisson regression problem, which I have been analysing in recent postings, to R.
There are two ways of implementing a Stata-R link; if you know the R language then you can code the R syntax directly into a commented-out section within your do file and export it to R in just the same way that we export a WinBUGS model file; on the other hand, if you want the R package to be available to users who only know Stata, then you have to write a Stata ado file that writes the R code for them.
It is instructive to start with a program that assumes some knowledge of R; next week we will see how we can hide the complexity. I will assume that you have R installed on your computer and that you have installed the package MCMCglmm by downloading it over the internet. This installation will also be hidden from the user in next week’s version.
I’ve discussed using a Stata-R link before in this blog and I am going to follow the same approach. You might find it helpful to read my original postings on this topic as they cover some of the basics in more detail. You can find them at,
https://staffblogs.le.ac.uk/bayeswithstata/2014/09/19/using-r-with-stata-part-i/
https://staffblogs.le.ac.uk/bayeswithstata/2014/09/26/using-r-with-stata-part-ii/
https://staffblogs.le.ac.uk/bayeswithstata/2014/10/03/using-r-with-stata-part-iii/
https://staffblogs.le.ac.uk/bayeswithstata/2014/10/10/using-r-with-stata-part-iv/
The data for our Poisson regression model describe the numbers of seizures experienced by 59 epilepsy patients in each of 4 consecutive 2 weeks periods. There are five explanatory variables and two random effects; one with a different level for each subject and one with a different level for each subject in each week. The problem was first introduced to this blog back in February https://staffblogs.le.ac.uk/bayeswithstata/2015/02/06/poisson-regression-with-two-random-effects/
MCMCglmm wants the data stacked into long columns with the four visits stored under one another. We could re-organize the data in R (R has a very neat package called dplyr that is designed specifically for data organization) but as we are primarily using Stata, we will prepare the data in Stata so that it is already in the format that MCMCglmm needs.
Here is the Stata code that centres the data, stacks it and saves it. In fact, MCMCglmm does not require us to centre the variables but, if I did not, then I would have to change the priors that I used in previous postings, so I have decided to centre for consistency.
use epilepsy.dta , clear
gen LB = log(Base/4)
qui su LB
gen cLB = LB – r(mean)
gen lnAge = log(Age)
qui su lnAge
gen clnAge = lnAge – r(mean)
gen BXT = LB*Trt
qui su BXT
qui gen cBXT = BXT – r(mean)
qui su Trt
gen cTrt = Trt – r(mean)
gen id = _n
gen zero = 0
gen one = 1
stack id y_1 cLB clnAge cTrt cBXT zero id y_2 cLB clnAge cTrt cBXT zero ///
id y_3 cLB clnAge cTrt cBXT zero id y_4 cLB clnAge cTrt cBXT one , ///
into(subject y base age trt bxt v4)
rename _stack visit
sort visit subject
save epilepsyforR.dta , replace version(12)
Notice that the data are stored in Stata 12 format, R cannot read Stata 13 or 14. Now all we need to do is to read these data into R and run MCMCglmm. Here is the R code that we need. To help avoid confusion, I will show R commands and output in green and Stata code and its output in blue.
library(foreign)
library(MCMCglmm)
D <- read.dta(file=”K/epilepsy /epilepsyforR.dta”)
prior <- list( B=list(mu=c(2.6,1,0,0,0,0),V=diag(1,6,6)),
G=list( G1=list(V=2/7,n=16) ),R=list(V=2/7,n=16) )
fit <- MCMCglmm(y ~ base+trt+bxt+age+v4,random= ~subject,
prior=prior,family=”poisson”,nitt=55000,burnin=5000,thin=5,data=D)
summary(fit)
The library() command (require() is an alternative that does much the same thing) loads two packages; foreign, which reads data files created by other programs and MCMCglmm, which provides our analysis.
This R code reads the Stata data file and stores the data under the name D. Then it defines the prior and runs the analysis storing the results under the name fit. The summary command prints a table of the estimates. In this case we get
DIC: 1157.116
G-structure: ~subject
post.mean l-95% CI u-95% CI eff.samp
subject 0.2607 0.1566 0.3778 4693
R-structure: ~units
post.mean l-95% CI u-95% CI eff.samp
units 0.1751 0.1189 0.2356 3639
Location effects: y ~ base + trt + bxt + age + v4
post.mean l-95% CI u-95% CI eff.samp pMCMC
(Intercept) 1.59213 1.42740 1.75384 5924 <1e-04 ***
base 0.91739 0.64866 1.17659 8145 <1e-04 ***
trt -0.76965 -1.52924 -0.01956 5279 0.046 *
bxt 0.25788 -0.12209 0.64963 6500 0.196
age 0.39816 -0.27944 1.07435 4970 0.256
v4 -0.09743 -0.27435 0.08035 5071 0.293
The estimates are similar to those given by WinBUGS.
Our next task is to understand the call to MCMCglmm, which is straightforward, and to understand the way that the priors are defined, which is not so straightforward.
The call to MCMCglmm almost explains itself. The fixed part of the model comes first and this is followed by the random effects; in this case I have a single random effect for each subject and the structure, R, defined in the prior provides the second random effect with a different value for each observation. The Poisson family is given a log-link by default. The analysis consists of 55000 iterations but the first 5000 of these are discarded and the remainder are thinned by only saving every 5th simulation.
The first thing to know when trying to understand the priors is that in MCMCglmm all families are given a residual variance structure, R, which in this case acts in addition to the randomness of the Poisson distribution. This residual variance is analogous to defining a random effect that takes a different value for each observation.
The other random effects are collectively called G and if there are many of them they are distinguished as G1, G2 … In this case we only define a random effect for each subject.
The priors on the variances of the random effects are inverse-Wishart distributions; one of the limitations of MCMCglmm is that it insists on this distribution as it is conjugate and simplifies the MCMC algorithm. When the random effects are independent, as they are here, they have a single variance and the multi-dimensional inverse-Wishart distribution reduces to an inverse-gamma. We need to understand this parameterization in order to set the priors.
MCMCglmm requires the user to parameterize the inverse-gamma prior by providing a guess at the true variance, V, and a parameter, nu, that expresses our certainty in the guess, a large value for nu and we are expressing strong belief in the accuracy of our guess at V.
The standard deviation of log(variance) is approximately sqrt(2/( nu-4)) so if we guess that V=3 and set nu=5 then we have 95% belief that the log(variance) will lie in the range log(3)±2sqrt(2) or equivalently that the variance will lie in the range exp(log(3)±2sqrt(2)) or between 0.2 and 50. Alternatively we could set nu=50 to reflect belief that the variance is most likely to be between 2 and 4.5.
Previously we worked with the Gamma distribution for the precision and set α=8 and β=1/2 so the expected precision was αβ=4 corresponding to a variance of ¼ and a standard deviation of ½. The equivalent inverse- gamma just inverts the β parameter giving α=8 and β=2. The IG has expected variance is β/(α-1)=2/7 corresponding to a standard deviation of 0.52 (remember that the average(variance) is only approximately 1/average(precision)).
In the example above I set V=2/7 and nu=16 to reflect belief that the variance lies between 0.13 and 0.65; this is quite informative but similar to my previous analyses of these data. This prior says that I believe that the standard deviation for the random effect will be in the range (0.36,0.80)
Next, we ought to make a tour of the presentation of these results, which I will not try to defend.
The two random variances (0.2607,0.1751) correspond to standard deviations (0.51, 0.42); very similar to those that we obtained by WinBUGS.
The idea of quoting 5 decimal places in the table of coefficients is fanciful, probably 2 decimal places are just about reliable given the number of iterations.
The effective sample size is another way of presenting the standard error of the mean. Here the mixing is such that a sample of 10,000 values after thinning acts like a random sample of 5071 when we estimate the coefficient of v4. The standard deviation of the simulated v4 coefficients was 0.09285 so had mixing been perfect so that the simulations were independent, the standard error would have been 0.09285/sqrt(10000)=0.0009285 but actually when we allow for the correlation it is 0.001285=0.09285/sqrt(n) where n is 5071.
The disadvantage of this presentation is that the sem is not easily derived so we cannot tell whether to trust 1,2,3,4 or 5 decimal places in the posterior means.
pMCMC is a complete cheat. It is not a p-value at all despite the stars that R uses to indicate significance, but rather it is twice the probability that the true value is above or below zero. So, in the 10,000 simulations v4 must have been negative most of the time but positive on 1465 iterations, giving a 0.1465 chance that it is +ve and pMCMC=2*0.1465=0.293. pMCMC does express our confidence in the sign of the coefficient but the presentation invites confusion.
The CI’s are not confidence intervals or even credible intervals but highest posterior density (HPD) intervals.
I’ve explained the output so that we can see the parallels between this analysis and the analyses that we obtained from WinBUGS and similar programs in previous postings. However, a Stata user need not rely on this presentation, they will read the raw results into Stata and they can summarise them in any way they choose.
The raw results are stored in the R list structure called fit. We could write this structure to a text file and then read all or part of that file into Stata. In my previous postings I presented two Stata ado files called rdescribe.ado and rextract.ado that enable us to read R lists from files. The full process comes in two stages first we must add a couple of lines to our R code in order to write fit to a file, then we use rdescribe and rextract to read it in Stata.
The extra R code is,
sink(“myout.txt”)
dput(fit)
sink()
The first call to the function sink() redirects output away from the screen and into a file and the second call returns output to the screen. dput() writes the contents of the structure fit. In fact, we will run R in the background so the default output goes to a log file and not to the screen.
To write the R script to a file and run it we can add the following lines to our Stata do file.
wbsmodel MCMCglmm.do MCMCglmm.R
/*
library(foreign)
library(MCMCglmm)
D <- read.dta(file=”E:/blog/topics/epilepsy/epilepsyforR.dta”)
prior <- list( B=list(mu=c(2.6,1,0,0,0,0),V=diag(1,6,6)),
G=list( G1=list(V=2/7,n=16) ),R=list(V=2/7,n=16) )
fit <- MCMCglmm(y ~ base+trt+bxt+age+v4,random= ~subject,
prior=prior,family=”poisson”,nitt=55000,burnin=5000,thin=5,data=D)
summary(fit)
sink(“myout.txt”)
dput(fit)
sink()
*/
execute R CMD BATCH MCMCglmm.R log.txt
This code uses the wbsmodel command that I wrote for creating WinBUGS model files to copy the R commands to a text file called MCMCglmm.R, then the commands are sent to R using my execute command. Instructions for downloading all of my commands are given at the end of this posting.
execute assumes that you have set up a file called executables.txt in your personal directory containing a line such as,
R,”Z:\Software\R-3.1.2\bin\x64\R.exe”
That is, it points to the location of the R.exe file on your system. The execute command sends the R output to log.txt. So in the log file you will find any error messages or, if everything works, you will find the results as produced by R’s summary(fit) command. The most convenient way to inspect the file is with the Stata command,
view log.txt
The raw numerical results are in myout.txt. R places a lot of information in the file and it is formatted as a complex list structure. To see what we have, give the Stata command,
rdescribe using myout.txt
and you will be told that we have,
Structures and sub-structures within file: myout.txt
Sol (matrix or set of variables)
Dim: 10000, 6
Lambda (single value)
VCV (matrix or set of variables)
Dim: 10000, 2
CP (single value)
Liab (single value)
Fixed (list)
formula (single value)
nfl (single value)
nll (single value)
Random (list)
formula (single value)
nfl (single value)
nrl (single value)
nrt (single value)
Residual (list)
formula (single value)
nfl (single value)
nrl (single value)
nrt (single value)
Deviance (matrix or set of variables)
DIC (single value)
X (single value)
Z (single value)
XL (single value)
error.term (single variable)
family (single variable)
Tune (single value)
Dim: 1, 1
The key information is held in Sol (presumably solution). This contains the 10000 simulations of the 6 regression coefficients. The variances of the random effects are in VCV.
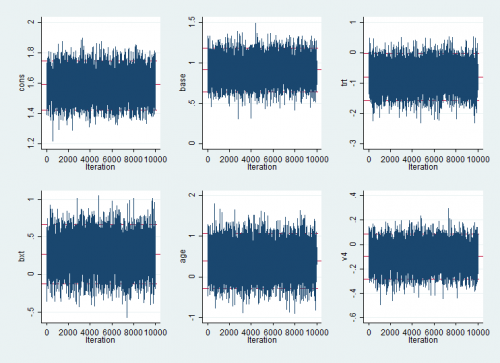
We can read Sol into Stata, rename the variables and plot them using the Stata commands
rextract using myout.txt, item(Sol) clear
rename Sol_1 cons
rename Sol_2 base
rename Sol_3 trt
rename Sol_4 bxt
rename Sol_5 age
rename Sol_6 v4
mcmctrace cons base trt bxt age v4
The mixing is excellent and in log.txt we will find that the timing was good also at about 18 seconds. Better than WinBUGS etc. although of course this program only fits glmms.
Next time I will present a Stata ado file that acts as an interface to MCMCglmm so that the Stata user does not need to know the R syntax.
If you want to download any of the programs referred to in this posting they are available from my webpage at https://www2.le.ac.uk/Members/trj


 Subscribe to John's posts
Subscribe to John's posts
Recent Comments