Here we go again
There has been quite a long gap since my last post because over the New Year and for a large part of January I was visiting my daughter who is working in Colombia. It was my first time in South America and I was immediately struck by the beauty and the vitality of the country. It was a refreshing change from visiting continental Europe, which appears tired and lacking in any sense of optimism. Columbia is definitely a country that is moving forward.
After such a gap it is natural to look back over last year’s postings and to think a little about the direction that the blog should take in the future. I notice that there has been a tendency for the topics that I cover to become more and more complex as time progresses. This is perhaps natural but it goes away from my reasons for writing the book. Bayesian Analysis with Stata was meant to be a guide to Bayesian analysis for a typical Stata user, by which I mean someone who is a user of statistical techniques but who is not a research statistician. I will try to correct the balance over the coming year by including more practical applications.
Downloading my programs and data
One of the problems that I had in the first year was that of making the software and data that I refer to available to readers. The blog itself can link to pdf files but not to files with any other format, so I can’t use it to make available the do, ado or dta files that I refer to. To make matters worse, my University has adopted a web protocol that Stata cannot read so I cannot post the code on my website and allow users to net install it in Stata.
There does not seem to be a totally satisfactory solution to this problem, but I have decided to add a page to my personal homepage (https://www2.le.ac.uk/Members/trj) called blog downloads and I will use this page to store zipped versions of the programs and data that I refer to. You will not be able to access them directly from within Stata as I would wish, but it will be a small job to download and unpack the files. As time allows I will do back over last year’s posting and add the code from those postings to the same webpage.
A Bayesian GLM with random effects
In the spirit of starting the year with something straightforward I thought that I would take a simple Bayesian model and fit it using Stata, Mata and then WinBUGS in order to re-establish the general approach. I have chosen to use the well-known epilepsy data of Thall and Vail and to fit a Poisson regression with two random effects. Of course, nothing is quite as simple as you expect and in turns out that this example throws up several interesting points, not least how best to program random effects in Stata.
The Model
The epilepsy data were introduced by Thall and Vail in 1990 (http://www.ncbi.nlm.nih.gov/pubmed/2242408) and come from a drug trial on 59 patients with epilepsy. The response is the count of the number of seizures that each subject has in each of 4 consecutive 2-week periods. The explanatory variables are the treatment, the total number of seizures in an 8 week period prior to treatment and the subject’s age. Because so many people have looked at these data, the form of the Poisson regression has become standardised and I will not attempt to revisit the form but just accept,
log(μ) = β0 + β1log(baseline/4)+ β2 trt + β3log(age) + β4trt*log(baseline/4) + β5v4 + u + e
where v4 is an indicator for the fourth visit, u is a subject specific random effect and e is a random effect with a different value for each visit of each subject. So u can be thought of as allowing for the unmeasured characteristics of the subject and e as allowing for the unmeasured events occurring to that person in that particular two-week period.
Most Bayesian analyses of these data have used very vague priors but since I do not really approve of such priors, I will opt for what I like to call realistically vague priors. Let us assume that prior to the trial we anticipate that the subject will have around one seizure per day so the two-week counts will be about 14. If we centre the covariates, then we would expect the constant to be about log(14)=2.6. I would anticipate that the coefficient of the baseline term (log(baseline/4) will be about 1.0 since this would imply no change between baseline and the trial. Finally I will centre the priors of the other regression coefficients on zero because I cannot confidently predict their direction of effect.
Assuming that people vary so that some average only one seizure every two weeks and some average 2 per day then log(μ) will range from 0 to 3.5, a variance of about 0.8 (sd about 0.9). If the linear predictor explains half of this variance then the random effect will have variance of about 0.2 each, which implies a standard deviation of 0.45. These of course are guesses but the standard deviations will not be 4.5 and are unlikely to be 0.045, so there is little point in making our priors ridiculously wide.
In the end I decided on,
Cons: β0 ~ N(2.6,1) log(base/4): β1~ N(1,1) Trt: β2 ~ N(0,1)
log(age): β3 ~ N(0,1) trt*log(base/4): β4 ~ N(0,1) V4: β5 ~ N(0,1)
Precision of u: τu ~ G(8,0.5) Precision of e: τe ~ G(8,0.5)
In fact my guesses are a little off target, the data suggest that typically people in the trial have about 1 seizure every two days and not one every day and the range is greater than I allowed for; some subject have hardly any seizures and the upper limit is higher than I anticipated with a few having over 50 within a single two week period. Of course, I cannot change my priors in the light of the data.
Calculating the posterior
Fitting this model is computationally quite challenging because as well as the 6 regression coefficients, β, we also have two variances and (4×59+59=295) values for the two random effects. Computation would be simpler is we were able to integrate the posterior over the 295 values of the random effects, but with a Poisson model this integration is not tractable so either we do in numerically or we estimate the 295 values as part of the analysis. The computation will be a particular challenge for Stata because it is slow relative to Mata and WinBUGS.
Analysis in Stata
The standard way that I use for fitting a Bayesian model in Stata is to place the values of all of the parameters in a row matrix. In this case, were we to pack all 303 parameters into a matrix, we would expect the resulting program to be slowed down by the repeated need to unpack the matrix. Probably we are not interested in the 295 values of the random effects and we would have integrated then out of the posterior had that been simple, so a convenient alternative would be place the 6 regression coefficients and the two precisions in a matrix but to place the values of the random effects in Stata variables. Only the first 8 parameter will be saved in the results file but the coding can be made much more efficient with vectors instead of matrices; this speeds up the program and makes for simpler code.
In the file epilepsy.dta, the data are stored in seven variables with one line for each person
y_1, y_2, y_3, y_4 = the counts for each of the four weeks
Base = the count for the baseline period
Trt = the treatment coded 0,1
Age = subject’s age in years
Let us start by centring the data. This should improve mixing.
use epilepsy.dta , clear
gen LB = log(Base/4)
qui su LB
gen cLB = LB – r(mean)
gen lnAge = log(Age)
qui su lnAge
gen clnAge = lnAge – r(mean)
gen BXT = LB*Trt
qui su BXT
qui gen cBXT = BXT – r(mean)
qui su Trt
gen cTrt = Trt – r(mean)
Next we will define variables to contain the 295 random effects. U will contain the 59 subject level effect and the E’s will contain the random effects for periods within subject. I’ll fill them with random starting values.
gen U = rnormal(0,0.5)
gen E1 = rnormal(0,0.5)
gen E2 = rnormal(0,0.5)
gen E3 = rnormal(0,0.5)
gen E4 = rnormal(0,0.5)
We will need a program to evaluate the log-posterior. The program below does the job although I have made no attempt to make it efficient.
program logpost
args logp b
local cons = `b'[1,1]
local base = `b'[1,2]
local trt = `b'[1,3]
local bxt = `b'[1,4]
local age = `b'[1,5]
local v4 = `b'[1,6]
local tU = `b'[1,7]
local tE = `b'[1,8]
scalar `logp’ = 0
tempvar eta mu1 mu2 mu3 mu4 LL
* log-likelihood of y_1 to y_4
gen `eta’ = `cons’ + `base’*cLB + `trt’*cTrt + `bxt’*cBXT + `age’*clnAge
gen `mu1′ = exp(`eta’ + U + E1)
logdensity poisson `logp’ y_1 `mu1′
gen `mu2′ = exp(`eta’ + U + E2)
logdensity poisson `logp’ y_2 `mu2′
gen `mu3′ = exp(`eta’ + U + E3)
logdensity poisson `logp’ y_3 `mu3′
gen `mu4′ = exp(`eta’ + `v4′ + U + E4)
logdensity poisson `logp’ y_4 `mu4′
* log-density of the random effects
local sdE = 1/sqrt(`tE’)
logdensity normal `logp’ E1 0 `sdE’
logdensity normal `logp’ E2 0 `sdE’
logdensity normal `logp’ E3 0 `sdE’
logdensity normal `logp’ E4 0 `sdE’
local sdU = 1/sqrt(`tU’)
logdensity normal `logp’ U 0 `sdU’
* priors
logdensity normal `logp’ `cons’ 2.6 1
logdensity normal `logp’ `base’ 1 1
logdensity normal `logp’ `trt’ 0 1
logdensity normal `logp’ `bxt’ 0 1
logdensity normal `logp’ `age’ 0 1
logdensity normal `logp’ `v4′ 0 1
logdensity gamma `logp’ `tU’ 8 0.5
logdensity gamma `logp’ `tE’ 8 0.5
end
As we will be working with some parameters in vectors rather than matrices, it makes sense to write our own sampler, which I will call mhsEPY because it is based on a Metropolis-Hastings algorithm. Let us reverse the natural order and see how it is called before we look at its contents.
matrix b = (2.6 , 1, 0, 0, 0 ,0 , 4, 4)
mcmcrun logpost b using mcmcepi.csv , ///
param(cons base trt bxt age v4 tauU tauE) ///
samp( mhsEPY , dim(8) ) ///
burn(5000) update(50000) thin(5) replace
The matrix b only contains 8 parameters so those are the only ones that are saved to the file mcmcepi.csv. We tell mcmcrun to update using mhsEPY and we say that it will update 8 parameters, while in fact it updates the 8 and then updates the 295 random effects. If you like, you can think of the updating of the random effects as a form of Monte Carlo numerical integration.
In my programs, samplers are called with three arguments; the name of the program for evaluating the log-posterior, the name of the matrix of parameters and the number of the first parameter to be updated at that stage. Here is my new sampler,
program mhsEPY
args logpost b ipar
local cons = `b'[1,1]
local base = `b'[1,2]
local trt = `b'[1,3]
local bxt = `b'[1,4]
local age = `b'[1,5]
local v4 = `b'[1,6]
local tauU = `b'[1,7]
local tauE = `b'[1,8]
*——————————
* Update first 8 parameters
*——————————
mhsnorm `logpost’ `b’ 1, sd(0.1)
mhsnorm `logpost’ `b’ 2, sd(0.1)
mhsnorm `logpost’ `b’ 3, sd(0.25)
mhsnorm `logpost’ `b’ 4, sd(0.1)
mhsnorm `logpost’ `b’ 5, sd(0.1)
mhsnorm `logpost’ `b’ 6, sd(0.1)
mhslogn `logpost’ `b’ 7, sd(0.3)
mhslogn `logpost’ `b’ 8, sd(0.3)
*——————————
* Update E1, E2, E3 , E4
*——————————
tempvar eta nu1 nu2 nu3 nu4 LL1 LL2 LL3 LL4 lu1 lu2 lu3 lu4 ///
newE1 newE2 newE3 newE4 nu1p nu2p nu3p nu4p newLL1 newLL2 newLL3 newLL4
gen `eta’ = `cons’ + `base’*cLB + `trt’*cTrt + `bxt’*cBXT + `age’*cAge
gen `nu1′ = `eta’ + S + E1
gen `LL1′ = -exp(`nu1′) + y_1*`nu1′ – 0.5*E1*E1*`tauE’
gen `newE1′ = E1 + rnormal(0,0.1)
gen `nu1p’ = `eta’ + S + `newE1′
gen `newLL1′ = -exp(`nu1p’) + y_1*`nu1p’ – 0.5*`newE1’*`newE1’*`tauE’
gen `lu1′ = log(runiform())
qui replace E1 = `newE1′ if `lu1′ < `newLL1′ – `LL1′
gen `nu2′ = `eta’ + S + E2
gen `LL2′ = -exp(`nu2′) + y_2*`nu2′ – 0.5*E2*E2*`tauE’
gen `newE2′ = E2 + rnormal(0,0.1)
gen `nu2p’ = `eta’ + S + `newE2′
gen `newLL2′ = -exp(`nu2p’) + y_2*`nu2p’ – 0.5*`newE2’*`newE2’*`tauE’
gen `lu2′ = log(runiform())
qui replace E2 = `newE2′ if `lu2′ < `newLL2′ – `LL2′
gen `nu3′ = `eta’ + S + E3
gen `LL3′ = -exp(`nu3′) + y_3*`nu3′ – 0.5*E3*E3*`tauE’
gen `newE3′ = E3 + rnormal(0,0.1)
gen `nu3p’ = `eta’ + S + `newE3′
gen `newLL3′ = -exp(`nu3p’) + y_3*`nu3p’ – 0.5*`newE3’*`newE3’*`tauE’
gen `lu3′ = log(runiform())
qui replace E3 = `newE3′ if `lu3′ < `newLL3′ – `LL3′
gen `nu4′ = `eta’ + `v4′ + S + E4
gen `LL4′ = -exp(`nu4′) + y_4*`nu4′ – 0.5*E4*E4*`tauE’
gen `newE4′ = E4 + rnormal(0,0.1)
gen `nu4p’ = `eta’ + `v4′ + S + `newE4′
gen `newLL4′ = -exp(`nu4p’) + y_4*`nu4p’ – 0.5*`newE4’*`newE4’*`tauE’
gen `lu4′ = log(runiform())
qui replace E4 = `newE4′ if `lu4′ < `newLL4′ – `LL4′
*——————————
* Update U
*——————————
tempvar nu LL newU newLL lu
gen `nu’ = `eta’ + U + E1
gen `LL’ = -exp(`nu’) + y_1*`nu’ – 0.5*S*S*`tauU’
qui replace `nu’ = `eta’ + U + E2
qui replace `LL’ = `LL’ -exp(`nu’) + y_2*`nu’
qui replace `nu’ = `eta’ + U + E3
qui replace `LL’ = `LL’ -exp(`nu’) + y_3*`nu’
qui replace `nu’ = `eta’ + `v4′ + U + E4
qui replace `LL’ = `LL’ -exp(`nu’) + y_4*`nu’
gen `newU’ = U + rnormal(0,0.1)
qui replace `nu’ = `eta’ + `newU’ + E1
gen `newLL’ = -exp(`nu’) + y_1*`nu’ – 0.5*`newU’*`newU’*`tauU’
qui replace `nu’ = `eta’ + `nU’ + E2
qui replace `newLL’ = `newLL’ -exp(`nu’) + y_2*`nu’
qui replace `nu’ = `eta’ + `newU’ + E3
qui replace `newLL’ = `newLL’ -exp(`nu’) + y_3*`nu’
qui replace `nu’ = `eta’ + `v4′ + `newU’ + E4
qui replace `newLL’ = `newLL’ -exp(`nu’) + y_4*`nu’
gen `lu’ = log(runiform())
qui replace S = `newS’ if `lu’ < `newLL’ – `LL’
end
Each of the parameters is updated in a M-H step so we have to find appropriate proposal distributions that produce good mixing and this will mean some trial and error while we play with the proposal standard deviations. In the code we take advantage of the conditional independence of the random effects, which means that we can run the updating calculations for the whole vector in one go.
I chose to run a burn-in of 5,000 and a run of 50,000 thinned to 10,000. So I needed 55,000 updates of the 303 parameters and in Stata this is not quick. On my desktop it took about 42 minutes, which equates to about 46 seconds for every 1,000 updates. I could probably save a lot of time by replacing the calls to logdensity with code for the normal and gamma log-densities but even then the code would still be quite slow and probably we should be using Mata or WinBUGS for such a large problem.
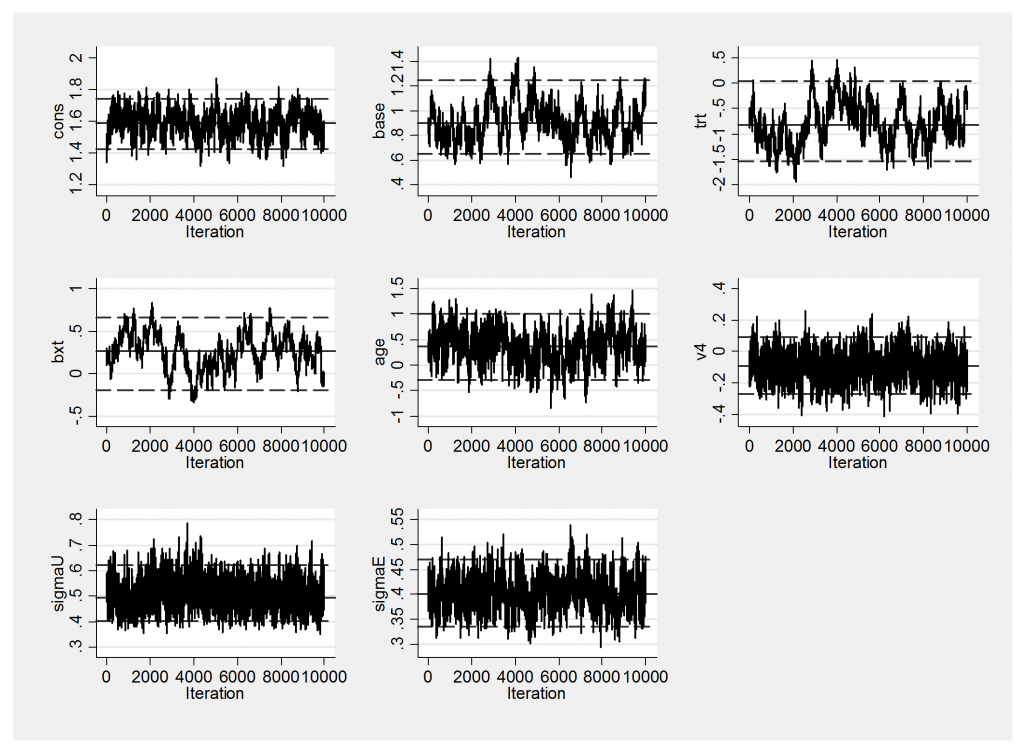
The trace plot is not very impressive
And this is reflected in the large standard errors on the baseline, the treatment effect and interaction between them.
----------------------------------------------------------- Parameter n mean sd sem median 95% CrI ---------------------------------------------------------- cons 10000 1.588 0.081 0.0037 1.589 ( 1.427, 1.738 ) base 10000 0.910 0.155 0.0145 0.898 ( 0.651, 1.251 ) trt 10000 -0.791 0.419 0.0526 -0.823 ( -1.540, 0.039 ) bxt 10000 0.257 0.219 0.0417 0.262 ( -0.194, 0.657 ) age 10000 0.363 0.335 0.0175 0.366 ( -0.294, 1.003 ) v4 10000 -0.091 0.091 0.0022 -0.090 ( -0.268, 0.089 ) sigmaU 10000 0.500 0.056 0.0010 0.495 ( 0.403, 0.622 ) sigmaE 10000 0.401 0.034 0.0009 0.401 ( 0.336, 0.471 ) ----------------------------------------------------------
In this table sigma=1/sqrt(tau).
Clearly his Stata program needs more work
(a) To make the code more efficient so that it runs faster
(b) To improve the mixing of the sampler
If this were a real problem rather than an illustrative example I would probably abandon Stata at this point and switch to Mata. However, that is a bit defeatist, so in my next posting I will return to the Stata code and try to improve it.
The data and programs for this analysis can be downloaded from https://www2.le.ac.uk/Members/trj by following the link to blog downloads.


 Subscribe to John's posts
Subscribe to John's posts
Recent Comments