Using R with Stata: Part I

In the posting before last I mentioned that there are many R packages that perform advanced statistical analyses for which there is no equivalent Stata command. In particular, I referred to the R package, DPpackage, that fits a range of Bayesian models with Dirichlet process priors.

Then in my last posting I introduced a problem of scatter plot smoothing and illustrated it with some data on IgG measurements made on children of various ages. In that posting I created a Bayesian solution entirely within Stata by using a Mata function for fitting finite mixtures of normal distributions.

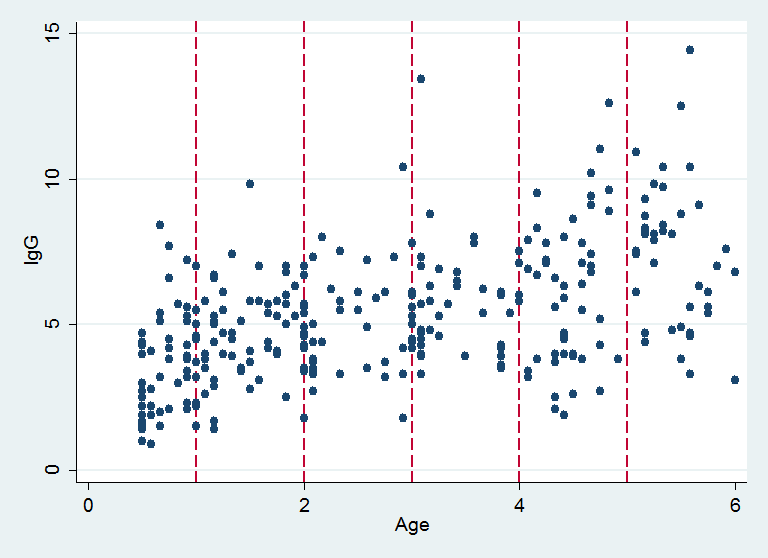
R’s DPpackage can also smooth a scatter plot and so this week I want to take the IgG data and show how a Stata user can make use of DPpackage. Here is a reminder of the structure of the data with vertical lines showing the ages at which I want to estimate the conditional distribution of IgG.

 

The R Code

The easiest way to see how a Stata user can take advantage of facilities in R is first to consider how we would use DPpackage if we were an R user. Here is a minimum set of R code that does the job.

setwd(‘E:/IGG’)
require(foreign)
require(DPpackage)
D <- read.dta(‘igg.dta’)
zbar <- c(7,3)
Sigma <- matrix(c(4,1,1,1),2,2)
MyPrior <- list(alpha=5, k0=0.25, nu1=10, m1=zbar, psiinv1=7*solve(Sigma))
MyDesign <- list(nburn=5000, nsave=5000, nskip=3, ndisplay=1000)
xp <- c(1,2,3,4,5)
fitIgG <- DPcdensity(y=D$igg, x=D$age, xpred=xp,ngrid=100,
compute.band=TRUE, type.band=”HPD”, prior=MyPrior, mcmc=MyDesign,
state=NULL, status=TRUE)

With apologies to anyone who already knows R, I will now run through this script and explain, line by line, what it does.

setwd(‘E:/IGG’)

This command sets the working directory and is equivalent to Stata’s command –cd-. A double quote could be used in place of the single quote; R allows both but it does not like back-slashes in the path, so avoid the default Windows notation E:\IGG.

require(foreign)
require(DPpackage)

In R, a package is a collection of programs and data. Stata’s programs are stored in ado files that are located automatically and loaded when they are needed, but this is not the case for packages in R and we have to request the packages that we want to use. I have done this with the require() command but many people use the library() command instead. They are equivalent.

Using packages is a two stage process in R. First the package must be installed over the internet and saved to the user’s hard-drive. This operation is done once. Subsequently it can be loaded using require(). This operation must be performed afresh in any session in which that package is needed. The initial package installation can be down with R’s install.package() command although it is easier to do it interactively by running R and using the menus. Later I will show that this too can be done from within Stata.

D <- read.dta(‘igg.dta’)

The foreign package contains a program called read.dta() that is able to read Stata’s .dta files. In R the symbol <- is used for assignment, where Stata would use = (actually, R also understands =. The fact that I use <- is both a reflection of the fact that I learnt R a long time ago and of my belief that <- is more logical). So the structure, D, contains the data that is read from the file igg.dta. D is a type of structure called a dataframe. This is a rectangular dataset that is equivalent to what one might see in Stata’s data editor. The difference is that in R you can have any number of dataframes in memory at the same time, while in Stata we are only allowed one.

zbar <- c(7,3)
Sigma <- matrix(c(4,1,1,1),2,2)
MyPrior <- list(alpha=5, k0=0.25, nu1=10, m1=zbar, psiinv1=7*solve(Sigma))

These commands set up the priors for the Bayesian analysis and store them in a structure called MyPrior. Let’s check the code and for the moment not worry about the numbers that I have chosen. zbar is a structure containing two numbers, like a mini-vector. Sigma is a symmetric 2 by 2 covariance matrix with diagonal elements 4 and 1 and off-diagonal 1. In R, a list is a very useful structure because it can contain other structures of mixed types. Here, the list, MyPrior, contains scalars, a vector and a matrix collected together under a single name. solve() is an R function for inverting a matrix.

MyDesign <- list(nburn=5000, nsave=5000, nskip=3, ndisplay=1000)

MyDesign is rather similar to MyPrior in that it is a list, this time a list describing the burnin and run length of the MCMC analysis. nskip controls the thinning; in this case we save a value then skip 3 iterations of the chain before saving another. The result is that the chain will need to run for 20,000 iterations in order to save our 5,000 simulations.

xp <- c(1,2,3,4,5)

xp is a vector containing the ages at which I want to estimate the conditional distribution of IgG, corresponding to the vertical lines in the plot above.

fitIgG <- DPcdensity(y=D$igg, x=D$age, xpred=xp, ngrid=50,
compute.band=TRUE, type.band=”HPD”, prior=MyPrior, mcmc=MyDesign,
state=NULL, status=TRUE)

DPcdensity is the program in the DPpackage that smooths a scatter plot and estimates conditional densities using a Dirichlet process prior. The results of the analysis are saved in a list structure called fitIgG and the items in the brackets are all of the options that I have chosen. Notice the use of the $ symbol. Within the dataframe, D, there are two columns called igg and age. We refer to igg within D as D$igg and age within D as D$age.

The options for the DPcdensity command specify x and y for the scatter plot, xpred sets the ages at which I want to estimate the conditional distributions and ngrid says that I want to evaluate them over a grid of 50 IgG values. Binary choices are denoted in R by TRUE or FALSE, so here I do want to calculate a 95% interval about my estimated conditional distribution and that band will be based on the HPD (highest posterior density) interval. The prior and mcmc design are set equal to my lists. The initial state is not specified (NULL) so the program will choose the initial values and finally the status is set to TRUE, which just means that we have a new run of the samplers and not a continuation of a previous run.

Finally, notice that the command that defines fitIgG runs over three lines but there is no continuation symbol similar to Stata’s /// nor is there an end of line marker similar to SAS’s semi-colon. R knows that the command is not finished because there is an unmatched bracket on the first line.

The Model

DPcdensity fits a Dirichlet process mixture (DPM) model which is slightly different from the Dirichlet process (DP) models that I have considered in previous postings. The model that is used is taken from,

Müller P, Erkanli A, West M
Bayesian curve fitting using multivariate normal mixtures
Biometrika 1996;83:67-79

Under this model each pair (IgGi,agei) is imagined to be drawn from a bivariate normal distribution with mean μi and covariance Σi. The pair (μi ,Σi) are selected from a Dirichlet process with a base distribution G0(μ,Σ) and so either a child is given the same mean and variance parameters as an existing child or they get a new set of parameters chosen from the base distribution. The natural clustering that we observe with the DP (for instance, in the Chinese restaurant algorithm), causes the children to group together into a small, but not fixed, number of bivariate distributions.

The concentration parameter of the DPM that Muller et al call alpha, will control the degree of clustering and hence the average number of distributions in the mixture. If we want the children to cluster into a small number of components then we will need to make alpha small so that there is a relatively small chance of starting a new cluster. Muller et al quote an approximation due to Antoniak that says that the number of components in a DPM will be approximately alpha*log(1+n/alpha). So if we set alpha=10 with a sample size of about 300 we can expect about 35 components each of about 8 or 9 children. In the end I opted for alpha=5.

Under this DPM the base distribution has two parts. One controlling the choice of a new cluster’s covariance matrix and the other controlling the choice of a new cluster’s mean. To make this pair conjugate with multivariate normal data and hence simplify the computation, the two parts are linked together. First, we choose the covariance matrix of the new cluster using a Wishart distribution with an expected covariance matrix Sigma, then we choose the mean of the new cluster from a multivariate normal distribution with covariance Sigma/k0, where k0 is a number that we must specify. This way there is only one prior covariance structure to specify.

From what we know about the ages of the children and about IgG measurements, let’s set the expected covariance matrix of each cluster to be Sigma = (4,1,1,1). The correlation will reflect the anticipated positive trend in the relationship and the standard deviations of IgG and age will be 2 and 1 respectively. The data range from (1,0.5) to (15,6) so to make the cluster means cover the area of the data we will need k0 to be small and I chose 0.25. This will make the standard deviations of the distribution of the mean about 2 times bigger than the standard deviations of the individual components (1/sqrt(0.25)≈2).

Finally, as R’s help for DPcdensity describes, the prior on Sigma is parameterized as an Inverse Wishart with expectation (df-p-1)*inv(Sigma) so, as we have bivariate data (p=2), if we set the parameter of the Wishart, called nu1, equal to 10 then we must set psiinv1 equal to 7*inv(Sigma).

I should mention that DPcdensity also allows hyperpriors on any of these parameters. For example, if we were not sure that alpha=5, then we could place a gamma prior on the value of alpha and allow the program to learn about the most appropriate value for alpha. This generalization does not affect the way that Stata communicates with R so I will not bother to set any hyperpriors.

Everything calculated by DPcdensity is saved in the list structure that I have named fitIgG. An R user would extract the things that interest them from this list and summarize them or plot them. As a Stata user, we want to write the contents of fitIgG to a file and then read them into Stata for further processing. There are two ways of doing this.

The first method for transferring the results is to extract them and rearrange them in R into rectangular sets of results that are easy for Stata to read.

The second method is to dump fitIgG to a text file and then write a general purpose Stata program that can read and extract information from a general R list.

Clearly the second method is the better way forward. Not only would we have access to all of the results, but the Stata extraction program could be used with any R list structure and not just with the results of DPcdensity. However, although this is the method that I use myself, the extraction program is not trivial, so I will describe that method at a later date.

For now let us just extract some of the information in R and write it to .dta files.

nClu <- as.data.frame(fitIgG$save.state$thetasave[,7])
names(nClu) <- “nclus”
write.dta(nClu,file=’nclusters.dta’)

This R code extracts the contents of column 7 of thetasave, which is a matrix stored in a list called save.state, which is itself stored in the list fitIgG. This column contains the number of clusters in the mixture at each of the 5,000 iterations of the sampler. The results are written to the Stata file nclusters.dta under the variable name nclus.

cDen <- as.data.frame(cbind(fitIgG$grid,t(rbind(fitIgG$densp.m,
fitIgG$densp.l,fitIgG$densp.h))))
names(cDen) <- c(“IgG”,”m1″,”m2″,”m3″,”m4”,”m5”,
        “l1″,”l2″,”l3″,”l4″,”l5″,”h1″,”h2″,”h3″,”h4″,”h5”)
write.dta(cDen,file=’cDensity.dta’)

Here we extract the plotting points for the conditional distributions at the 5 ages that we specified. The distributions are evaluated across a grid of 50 points. m is the mean estimate and (l,h) represents the 95% interval. They need to be transposed and bound together into a dataset that has 50 rows and 16 columns so that they fit neatly in a .dta file.

Now I have a rule with my postings, I try to keep the length to about 1,000 words but on no circumstances am I to go over 1,500. This is partly to protect my time and partly to protect the reader. I have now exceeded my upper limit by quite a margin, so I will stop and resume next time by looking at the same problem from the perspective of a Stata user rather than an R user.