In recent postings I have analysed the epilepsy trial of Thall and Vail using Stata, WinBUGS, OpenBUGS and JAGS and after a brief diversion last week I now want to move on to analysing the data using Mata. Previously we saw that an analysis in Stata takes about 6 minutes, while the BUGS-like programs take about 2 minutes and give better mixing. Our challenge will be to prepare a Mata program that can rival WinBUGS, OpenBUGS and JAGS for speed and mixing.
I have not written much about the use of Mata in this blog so I am going to take this opportunity to start with a very straightforward Mata program and to talk in some detail about how it is put together. Later I will consider ways of improving the efficiency.
Let me just recap the model that we want to fit. The data were introduced by Thall and Vail in 1990 (http://www.ncbi.nlm.nih.gov/pubmed/2242408) and come from a drug trial on 59 patients with epilepsy. The response is the count of the number of seizures that each subject has in each of 4 consecutive 2-week periods. The explanatory variables are the treatment, the total number of seizures in an 8 week period prior to treatment and the subject’s age. Because so many people have looked at these data, the form of the Poisson regression has become standardized and I will not attempt to revisit the form but just accept,
log(μ) = β0 + β1 log(baseline/4)+ β2 trt + + β3 trt*log(baseline/4 + β4 log(age)) + β5 v4 + u + e
where μ is the Poisson mean, v4 is an indicator for the fourth visit, u is a subject specific random effect and e is a random effect with a different value for each visit of each subject. So u can be thought of as allowing for the unmeasured characteristics of the subject and e as allowing for the unmeasured events occurring to that person in that particular two-week period.
The algebra for calculating the log posterior is simple but rather long for inclusion in this posting so I have set it out in a pdf that can be viewed by clicking on epilepsyequations.
In a small problem for which efficiency is not a major concern, we might program the model by packing all of the parameters into a single row vector and then cycling through them one at a time. In this case there are 6 regression coefficients, two variances for the random effects and 5×59=295 values of the random effects; a total of 303 parameters so we might anticipate that updating one at a time is going to be rather inefficient. None the less, that is where I am going to start.
The best way of programming this problem is to write the data handling and the control of the algorithm in Stata but to program the calculation of the log-posterior in Mata. So let us first look at the Stata code that controls the calculations. This code is almost identical to that used when we solved the problem only using Stata. It is,
*————————————-
* Block A: read data
*————————————-
use epilepsy.dta , clear
gen LB = log(Base/4)
qui su LB
gen cLB = LB – r(mean)
gen lnAge = log(Age)
qui su lnAge
gen clnAge = lnAge – r(mean)
gen BXT = LB*Trt
qui su BXT
qui gen cBXT = BXT – r(mean)
qui su Trt
gen cTrt = Trt – r(mean)
*————————————-
* Block B: set initial guess
*————————————-
matrix theta = J(1,303,0)
matrix theta[1,1] = 2.6
matrix theta[1,2] = 1
matrix theta[1,7] = 4
matrix theta[1,8] = 4
forvalues i=9/303 {
matrix theta[1,9] = rnormal(0,0.5)
}
matrix s = J(1,303,0.1)
*————————————-
* Block C: run the analysis
*————————————-
mcmcrun logcpost X theta using epilepsymata.csv , ///
param(cons base trt bxt age v4 tauU tauE u1-u59 e1-e236) ///
samp( 6(mhsnorm , sd(s)) 2(mhslogn , sd(s)) 295(mhsnorm , sd(s) ) ) adapt ///
burn(5000) update(50000) thin(5) replace ///
data(X=(y_1 y_2 y_3 y_4 cLB cTrt cBXT clnAge) theta s) mata
*————————————-
* Block D: summarize the results
*————————————-
insheet using epilepsymata.csv, clear case
gen sigmaU = 1/sqrt(tauU)
gen sigmaE = 1/sqrt(tauE)
mcmctrace cons base trt bxt age v4 sigmaU sigmaE
mcmcstats cons base trt bxt age v4 sigmaU sigmaE, corr
Let us work through this block by block. In block A we read the data and centre the explanatory variables in order to improve mixing. In block B we set up a row vector containing the initial values; I have ordered the parameters as, 6 regression coefficients, 2 precisions, 59 subject-level random effects (u) and 4×59 visit by subject random effects (e). I also set up a row vector called s containing the proposal standard deviations for my Metropolis-Hastings samplers. In block C we call mcmcrun to control the updating; this is the only command that changes when we use Mata. I will discuss the changes in a moment but meanwhile let us note that block D analyses the results and is the same whether we use Mata or Stata.
Now let us dissect the call to mcmcrun. First notice that the mata option is set so mcmcrun will write and execute a piece of Mata code for performing the analysis and that code will expect to find a Mata program for calculating the log posterior. So in a moment we will need to write it. Directly after the command word we place the name of our Mata function, in this case I will call in logcpost, followed by the name of a Mata matrix containing the data and the name of the row vector that contains the initial values. At present X does not exist and theta is a Stata matrix so we have to pass this information into Mata; this is done by the data option. Here you will see that we take the response data y_1, y_2 y_3 y_4 and the explanatory variables and we pack them into X, then X along with theta and s are passed from Stata to Mata. As a result we will be able to refer to the Mata versions of these structures in our Mata code.
The other options are no different to what we would use with a Stata program. I used a normal random walk Metropolis-Hastings algorithm for the regression coefficients and the random effects and I use a log-normal proposal for the precisions. There will be a burnin of 5,000 followed by 50,000 updates thinned to 10,000 by storing every 5th value. The updates will be stored in the file epilepsymata.csv under the names given in the param option and finally we will adapt the proposal standard deviations during the burnin to try and improve efficiency.
Our remaining task is to write some Mata code that evaluates the log-posterior. This can be stored in the same do file and placed anywhere before block C, usually I place the Mata code at the very start. Here is a piece of Mata code that does the job.
mata:
mata clear
real scalar logcpost(real matrix X,real rowvector t,real scalar p)
{
real scalar etai, etai1, etai2, etai3, etai4, i, logL
real colvector eta, eta1, eta2, eta3, eta4
if( p < 7 ) {
eta = t[1]:+t[2]:*X[,5]:+t[3]:*X[,6]:+t[4]:*X[,7]:+t[5]:*X[,8]:+t[|9\67|]’
eta1 = eta + t[|68\126|]’
eta2 = eta + t[|127\185|’
eta3 = eta + t[|186\244|]’
eta4 = eta + t[|245\303|]’ :+ t[6]
logL = sum( -exp(eta1) + X[,1]:*eta1 -exp(eta2) + X[,2]:*eta2 -exp(eta3) + X[,3]:*eta3 -exp(eta4) + X[,4]:*eta4 )
if( p == 1 ) return(logL – 0.5*(t[1]-2.6)*(t[1]-2.6))
else if( p == 2 ) return(logL – 0.5*(t[2]-1)*(t[2]-1))
else if( p == 3 ) return(logL – 0.5*t[3]*t[3])
else if( p == 4 ) return(logL – 0.5*t[4]*t[4])
else if( p == 5 ) return(logL – 0.5*t[5]*t[5])
else if( p == 6 ) return(logL – 0.5*t[6]*t[6])
}
else if( p == 7 ) return( -0.5*t[7]*t[|9\67|]*t[|9\67|]’ + 29.5*log(t[7]) + 7*log(t[7]) – 2*t[7] )
else if( p == 8 ) return( -0.5*t[8]*(t[|68\126|]*t[|68\126|]’+t[|127\185|]*t[|127\185|]’
+t[|186\244|]*t[|186\244|]’+t[|245\303|]*t[|245\303|]’) + 118*log(t[8]) + 7*log(t[8]) – 2*t[8] )
else if( p >=9 & p <= 67 ) {
i = p – 8
etai = t[1]:+t[2]:*X[i,5]:+t[3]:*X[i,6]:+t[4]:*X[i,7]+t[5]:*X[i,8]+t[p]
etai1 = etai + t[p+59]
etai2 = etai + t[p+118]
etai3 = etai + t[p+177]
etai4 = etai + t[p+236] + t[6]
return( -0.5*t[7]*t[p]*t[p] – exp(etai1) + X[i,1]*etai1 – exp(etai2) + X[i,2]*etai2
– exp(etai3) + X[i,3]*etai3 – exp(etai4) + X[i,4]*etai4 )
}
else if( p >= 68 & p <= 126 ) {
i = p – 67
etai = t[1]+t[2]*X[i,5]+t[3]*X[i,6]+t[4]*X[i,7]+t[5]*X[i,8]+t[p-59]+t[p]
return( -0.5*t[8]*t[p]*t[p] -exp(etai) + X[i,1]*etai )
}
else if( p >= 127 & p <= 185 ) {
i = p – 126
etai = t[1]+t[2]*X[i,5]+t[3]*X[i,6]+t[4]*X[i,7]+t[5]*X[i,8]+t[p-118]+t[p]
return( -0.5*t[8]*t[p]*t[p] -exp(etai) + X[i,2]*etai )
}
else if( p >= 186 & p <= 244 ) {
i = p – 185
etai = t[1]+t[2]*X[i,5]+t[3]*X[i,6]+t[4]*X[i,7]+t[5]*X[i,8]+t[p-177]+t[p]
return( -0.5*t[8]*t[p]*t[p] -exp(etai) + X[i,3]*etai )
}
else if( p >= 245 & p <= 303 ) {
i = p – 244
etai = t[1]+t[2]*X[i,5]+t[3]*X[i,6]+t[4]*X[i,7]+t[5]*X[i,8]+t[6]+t[p-236]+t[p]
return( -0.5*t[8]*t[p]*t[p] -exp(etai) + X[i,4]*etai )
}
}
end
Let’s go through this in some detail as it would act as a model for other problems.
Line 1 tell Stata that we are about to provide some Mata code. Line 2 clears anything already in Mata, this is only necessary if you have been using Mata for other calculations, when Mata is first called it is empty anyway. On line 3 we start the function that calculates the log-posterior. In Mata a function can return a value or a matrix or a string and in this case it will return the value of the log-posterior, which is a real scalar i.e. a single number. We pass information into our functions in the form of our data matrix X, the row vector of current parameter values, which inside this function I call t, and a scalar denoting the number of the parameter that is currently being updated. This is the order expected by the Mata program that mcmcrun will create for performing the updates so we cannot alter it, although you can use different internal names for the arguments if you wish.
The contents of the function are enclosed in curly brackets { } and once we have defined our Mata function we use the end command to leave Mata and return control to Stata.
Following the call we list the scalars and column vectors that will be used in the calculations. This is not essential as Mata is quite smart and will work out what’s a scalar and what’s a vector as it goes along. Providing this information can speed up the program very, very slightly but it also helps protect us from programming errors, for example, should a matrix calculation not produce a column vector when one is expected, the compiler will flag the error. Defining the structures in this way is called the strict form of Mata, if we do not define them and instead want to rely on Mata to do the work, then we must switch this off by issuing the Stata command,
set matastrict off
before entering Mata.
The calculations themselves are divided into sections depending on the type of parameter that is being updated. So p<7 refers to the six regression coefficients, p==7 and p==8 are the two precisions and so on. The formulae that are being programmed are detailed in the downloadable pdf epilepsyequations and the code for the calculations is reasonably self-explanatory although a couple of points are worth noting.
t[1]:+t[2]:*X[,5]:+…. In a few places we want to perform calculations that combine scalars and vectors; here, for example, we want to add the scalar t[1] to all of the values in the row vector formed by multiplying column 5 of X (the centred log baseline values) by t[2]. We can create term by term sums and products with the colon notation, :+ or :*, while without the colon we create normal matrix addition and multiplication in which numbers of rows and columns need to match appropriately.
t[|9\67|]… This notation is a convenient way of extracting a subvector from a larger vector. In this case we are extracting parameters 9 to 67, that is to say the 59 values of the random effect u.
This completes the programming task, the Metropolis-Hastings samplers are pre-programmed in the libmcmc library created by running the downloadable program mcmclibrarymata.do. The Mata program that calls the chosen samplers and saves the updates in written for us by mcmcrun and then automatically compiled and run. So we get the results just as if we had used Stata, but hopefully in quicker time.
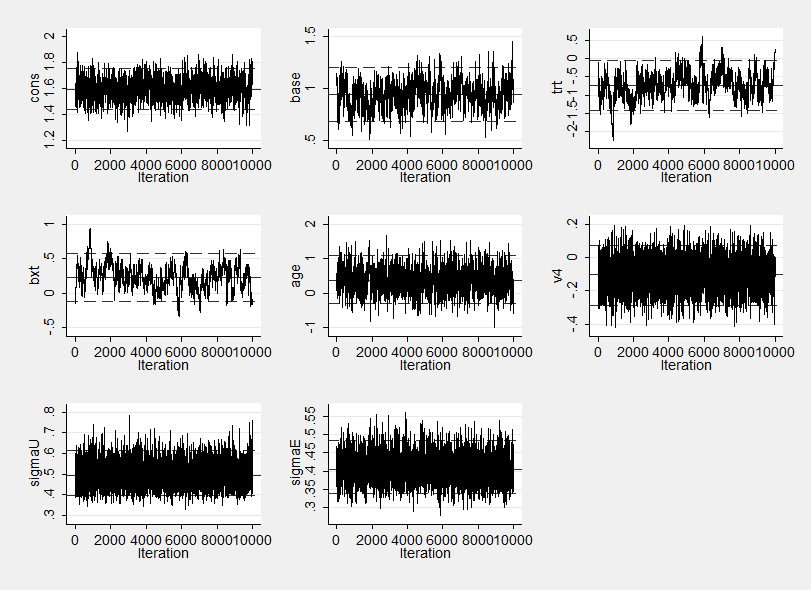
Here are the estimates based on the simulated marginal posteriors and the trace plot.
---------------------------------------------------------------------------- Parameter n mean sd sem median 95% CrI ---------------------------------------------------------------------------- cons 10000 1.595 0.080 0.0032 1.594 ( 1.435, 1.756 ) base 10000 0.940 0.129 0.0084 0.941 ( 0.683, 1.207 ) trt 10000 -0.733 0.357 0.0316 -0.734 ( -1.407, -0.057 ) bxt 10000 0.236 0.180 0.0224 0.238 ( -0.121, 0.575 ) age 10000 0.387 0.351 0.0139 0.375 ( -0.281, 1.097 ) v4 10000 -0.102 0.092 0.0020 -0.100 ( -0.286, 0.076 ) sigmaU 10000 0.497 0.056 0.0009 0.494 ( 0.399, 0.617 ) sigmaE 10000 0.407 0.037 0.0009 0.404 ( 0.339, 0.485 ) ----------------------------------------------------------------------------
The program takes about 3 minutes to run and so is quicker than Stata but slower than BUGS. I am sure that we can speed this up with more efficient code but the major issue is the poor mixing reflected in the comparatively large sems and the strong autocorrelation in some of the trace plots. Next week I will adapt the Mata code to try to address these issues.
The data and code referred to in this posting can be downloaded from my home page at https://www2.le.ac.uk/Members/trj


 Subscribe to John's posts
Subscribe to John's posts
Recent Comments