When I started this blog I decided to try and post once a week for the first few months and so I has to plan ahead. I found that there were many topics that I wanted to cover that involved multivariate normal models for which the conjugate prior on the precision matrix is a Wishart distribution. Now I have already explained (Why I don’t use WinBUGS priors) that I am not a fan of very vague priors, so over the coming weeks I will need to set informative Wishart priors and I thought that I would dedicate this posting to the general problem of specifying this type of prior.
To illustrate the problem, I performed a small experiment in which I generated some random values from a two dimensional Wishart distribution. Here is the code from a Stata do file that does the job. The program is written using Stata commands but it calls WinBUGS to perform the simulation. The program uses several of the downloadable wbs programs that are described in the book ‘Bayesian Analysis with Stata’ that will be published in a few weeks time.
wbsmodel wishartsim.do model.txt
/*
model {
T[1:2,1:2] ~ dwish(R[1:2,1:2],DF)
}
*/
local DF = 5
matrix B = (1, 0.5 \ 0.5, 1)
matrix T = syminv(B)
matrix R = `DF'*B
wbslist (matrix R) (DF=`DF') using data.txt, replace
wbslist (matrix=T) using init.txt , replace
wbsscript using script.txt , replace set(T) update(1000) ///
model(model.txt) data(data.txt) init(init.txt) coda(out) ///
log(log.txt)
wbsrun using script.txt
type log.txt
wbscoda using out , clear
gen v1 = .
gen v2 = .
gen rho = .
forvalues i=1/1000 {
matrix T[1,1] = T_1_1[`i']
matrix T[1,2] = T_1_2[`i']
matrix T[2,1] = T_2_1[`i']
matrix T[2,2] = T_2_2[`i']
matrix V = syminv(T)
qui replace v1 = V[1,1] in `i'
qui replace v2 = V[2,2] in `i'
qui replace rho = V[1,2]/sqrt(V[1,1]*V[2,2]) in `i'
}
histogram rho , start(-1) width(0.05)
T is the precision matrix (inverse of the covariance matrix) that follows the Wishart distribution and R and DF are the two parameters that the user has to choose when setting a prior. WinBUGS is used to simulate 1000 random matrices and then each one is inverted and the variances and correlation are extracted. The command wbsmodel was discussed in one of my previous postings under the title keeping good records.
Keep in mind that there are two commonly used parameterizations of the Wishart. I have followed WinBUGS in parameterizing in terms of a matrix R and a scalar DF, but many people parameterize in terms of the inverse of R and the scalar DF.
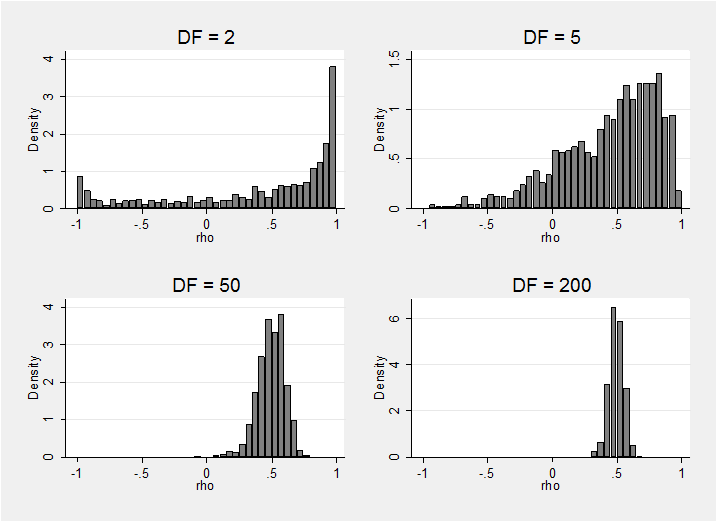
I ran the program with different values for the degrees of freedom, DF, and matrix R=DF*(1,0.5.5,1) and then I created the following histograms of the simulated correlations, rho. Mathematically, DF cannot be less than the dimension of the precision matrix, so I start with DF=2.
Clearly, the larger the parameter DF, the stronger is the user’s prior. The basis matrix from which R is formed, i.e. B=(1, 0.5\ 0.5, 1), is a guess at the covariance matrix, so in this case we start with the belief that the variances are one and the covariance is 0.5, which implies that rho is also 0.5. We can see that as DF increases so our beliefs concentrate around that value. However, the parameter that must be set in the Wishart is not B itself but R=DF*B.
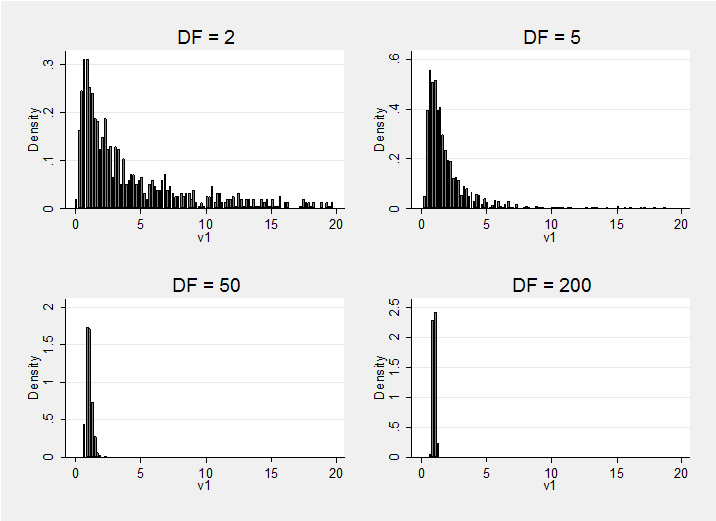
I also plotted histograms for the variances of the first variable and as before the distribution of prior beliefs concentrates around the value in the basis matrix, in this case converging to 1. I have truncated the xaxis of these histograms at 20 and in the case of DF=2 this has excluded a few extremely large values. People who favour vague priors need to keep this in mind because when DF is low, the sampler will try some very extreme (perhaps unbelievable) variances and these could cause numerical problems.
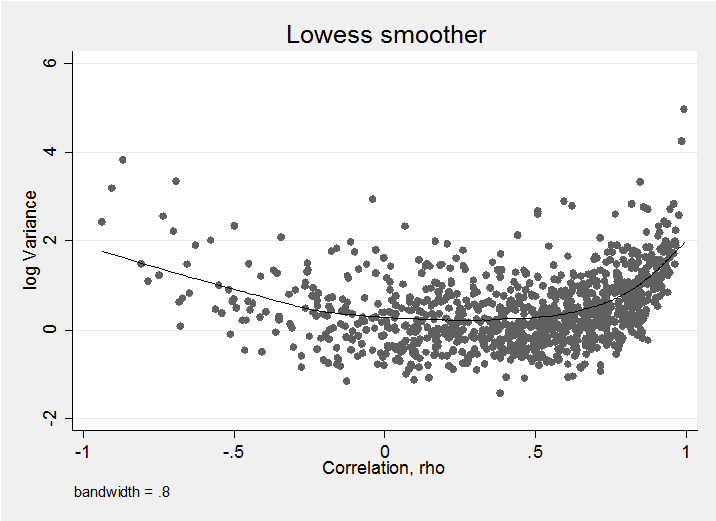
Finally we need to be aware that the simulated variances and correlations will not be independent. Here is a plot of the log-variance against correlation for DF=5.
As the lowess trend line emphasises, when rho is close to 1 or -1 the variance is noticeably larger than it is in the centre of its range. Some people have taken this pattern as grounds for criticising the use of the use of the Wishart but for me, the important point is that seeking independence is a bit like seeking a uniform prior for one of the parameters; even is you achieve it, it only applies to that particular parameterization and a transformation to a new scale will destroy the uniformity and/or the independence. So if we were to find a distribution that made the correlation and variance independent, this would still leave us with a relationship between say, the variance and covariance.
The real question is, does the pattern of the Wishart distribution reasonably approximate your actual prior beliefs? if not, then find another distribution but don’t expect to find one where everything is independent and uniformly distributed.
One of the difficulties with the Wishart is that there is only one parameter to describe the strength of our beliefs and this has to apply to the whole matrix, so we cannot be more certain about some variances than others. Instead we are forced to compromise.
Imagine that we have decided that we want to centre our beliefs on B=(1, 0.5\ 0.5, 1) and now we want to choose DF. If we believe that the variances will, almost certainly, be less than 5 then our extreme case is Bmax=(5, 2.5\ 2.5, 5). This implies precision matrices T=inv(B) = (1.33, -0.66\-0.66, 1.33) and Tmin= inv(Bmax) = (0.27, -0.13\-0.13, 0.27).
The range of precisions between the centre and the minimum is 1.33 to 0.27, so the standard deviation of the precision must be about half that range, or 0.55. According to the delta method, the standard deviation of a precision is approximately mean(precision)*sqrt(2/DF), so 0.55=1.33sqrt(2/DF) and we need to choose DF to be about 12.
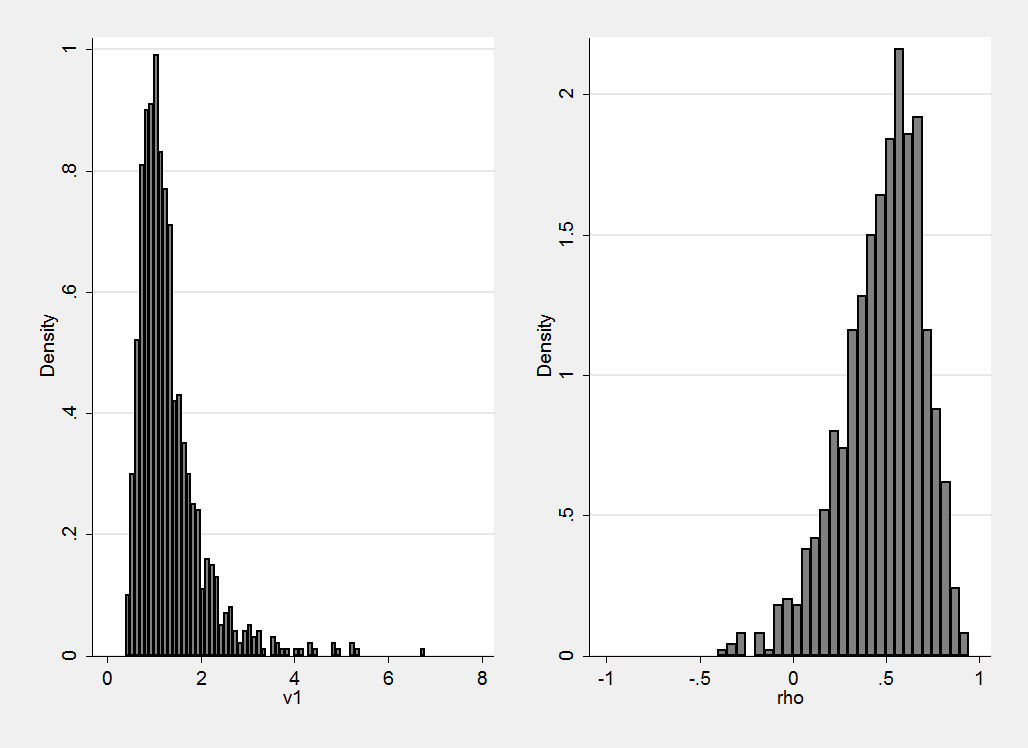
Here are the simulations of a Wishart distribution with B=(1, 0.5\ 0.5, 1) and DF=12. The variance has the property that we wanted and we would have to be willing to accept the consequential prior on the correlation.
If in doubt, simulate some data and do the experiment.


 Subscribe to John's posts
Subscribe to John's posts
I like what you guys are usually up too.
This type of clever work and exposure! Keep up the excellent works guys
I’ve included you guys to my personal blogroll.
Thanks, your comments help encourage me to continue the blog