Solutions to the Exercises: Chapter 1

I usually set my students open-ended questions but I like to break down the tasks in order to help them structure their answers.  Anyway, whatever the merits of this type of questioning, that approach has certainly influenced the exercises that I have given at the end of each chapter of ‘Bayesian analysis with Stata’ and because many of those exercises are open-ended, I do not have model answers. However, it seems reasonable that I should admit to my limitations by trying to answer my own questions. Here are my attempts at the relatively straightforward questions about prior distributions given at the end of chapter 1. Periodically, I’ll return to the exercises from the book and work my way through the other chapters.

In this posting there are two graphs, you can download the Stata code that I used to create the plots from solution1code.

Question 1:

The first question addresses the issue of what you should do if it turns out that someone’s prior is completely at odds with the data. Specifically I asked,

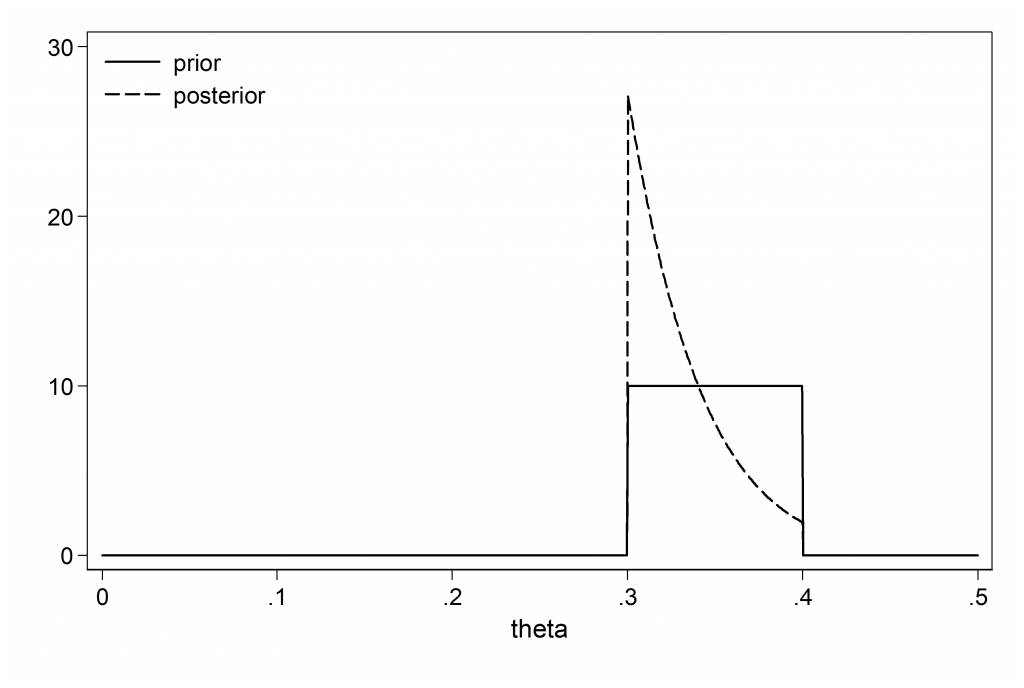
An expert tells you that the prior probability of an event occurring can be described as uniform between 0.3 and 0.4. You conduct an experiment and find that the event occurs only once in twenty occasions.

(i) Sketch the shapes of the prior and posterior distributions

The question asked for an approximate, free-hand sketch but in a blog it is easier for me to plot the curves.

(ii) In the light of the data, was the prior reasonable?

Depends what you mean by reasonable. Presumably the researcher had good reason to select such a restrictive prior and anyway it is too late to change it now. You have to live with your priors, so allocating zero probability outside of 0.3 to 0.4 was a high-risk strategy.

(iii) Would you be willing to use predictions based on this posterior?

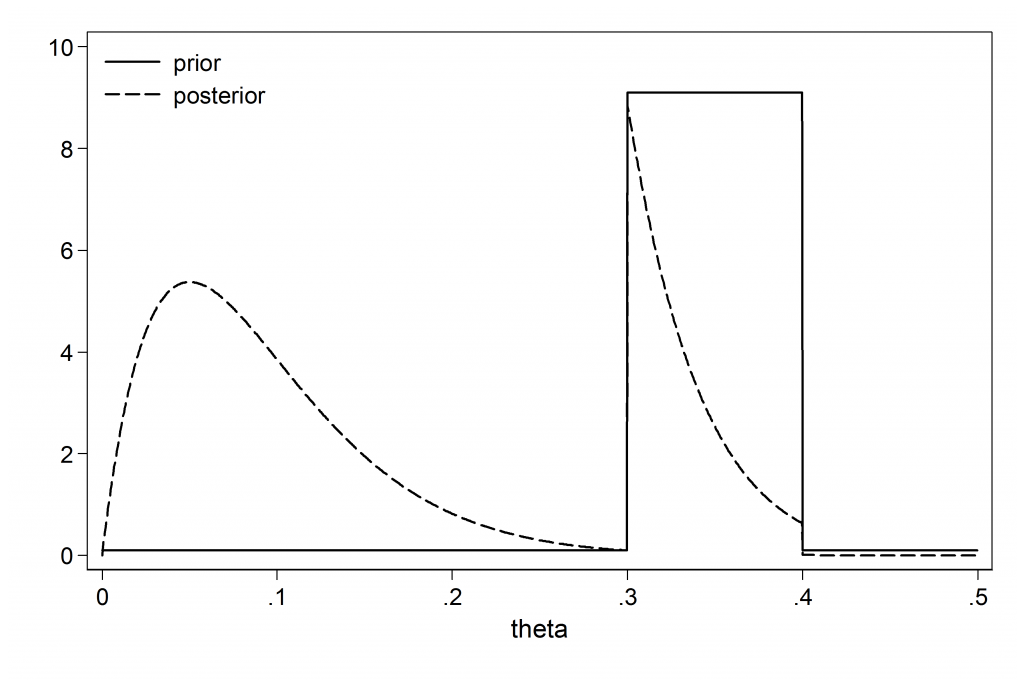
Personally no, but then I would not have used a prior that excludes theoretically possible values.This is one of those situations in which no amount of data can ‘correct’ or ‘dominate’ the prior. Consider what would have happened had the expert reserved some of their probability for the full (0,1) range. In the plot below the prior puts 90% of the probability over the range 0.3 to 0.4 and the rest uniformly across (0,0.3) and (0.4,1).

The posterior is bimodal and reflects our surprise on seeing the actual data. With this prior the data would dominate if the sample size were large enough.

(iv) Would it be reasonable to ask the expert to reassess his or her prior?

Too late for that – all you can do is use these data to better inform your next study

Question 2:

The second question addresses the issues that arise if you ask someone to formulate a prior when they are already aware of the data. Problems of this type are not infrequent, for instance how do you get an expert to set the prior in a meta-analysis when the expert’s opinion will be partly based on the studies that you wish to pool. In the actual example I asked about priors for a model that is to be used for predicting a time series.

A model is devised for predicting movements in the exchange rate between the euro and the dollar. The intension is to fit the model to data from the last twelve months and then to use the model to make predictions.

(i) Is it possible for an expert to give informative priors for the parameters in the model that are not already influenced by the data you hope to analyse?

An expert would be a poor source of priors for this model. Personally, I doubt if expert opinion could ever be used with this type of retrospective data.

(ii) How might you obtain priors for this problem?

One option would be to use vague (non-informative) priors but that way you remove most of the benefit of adopting the Bayesian approach. You could perhaps use vague priors to analyse some historical data, (maybe data from the year before last) and then use the results of that analysis as the prior for the current analysis. This would be very similar to redesigning your study so as to base your predictions on data from the last 24 months. We must be open to the possibility that there are some problems were informative priors cannot be used.

Question 3:

Question 3 considers whether people’s beliefs are well expressed as probabilities. Sadly, people are often irrational. In this example the awkward expert is trying to assess pollution in a city centre.

An expert gives their prior distribution for the average daily sulphur dioxide level at a particular point in the centre of town. You measure the sulphur dioxide level daily for a week and use a Bayesian analysis to obtain the posterior distribution. When you show the data and the posterior distribution to the expert, he refuses to accept your analysis and draws a completely different distribution saying that, having seen the data, this is what he now believes.

(i) Why might your calculation and the expert’s sketch disagree?

People are strange and they do not actually update their opinions according to Bayes theorem, some are more conservative than others and some are quick to change their mind. A person whose opinions really do follow the rules of probability is described as coherent, so we could dismiss this expert as incoherent. Insulting the expert might make us feel better but it would not really address the problem.

(ii) Which distribution better describes the expert’s updated beliefs, your posterior or his sketch?

Probably the sketch.

(iii) If you reject the posterior, can you ever again be sure that a posterior distribution describes an updated opinion?

It is doubtful whether posterior distributions do actually describe people’s updated beliefs, what they give is a rational updating of the prior, but people are not rational.

(iv) If you reject the sketch, what confidence can you have in the prior that the expert drew?

In a Bayesian analysis the prior forms part of the model. So, as in all statistics, it is implicit that the conclusions are conditional on the model, which in a Bayesian analysis also means conditional on the prior. We might say, ‘If the data are well approximated by this mathematical model and if your prior beliefs are well approximated by this function, then this is what a coherent person would conclude’. We would certainly be concerned if small changes in the prior led to different conclusions, but the same could be said for any of the assumptions implicit in the mathematical part of the model.

Question 4:

Finally I asked about the setting of priors under a constraint. This question was meant as a step towards the general issue of eliciting expert opinion when parameters cannot be treated as independent.

A researcher wishes to estimate the proportions of different types of terrain using aerial photographs of sample areas. They agree to classify the terrain as forest, grassland or other and for a particular region give prior estimates of the percentages as 60%, 30%, 10% and when you ask them about their uncertainty they say that all prior estimates are accurate to within ±10%, that is to say they believe the percentages to lie within the ranges (50%,70%), (20%,40%) and (0%,20%)Further they believe that within those ranges all percentages are equally likely

(i) Why do these figures not describe a prior distibution?

If the first two percentages are 65% and 30% then the last one cannot be uniform(0,20). You can only place probability over combinations that sum to 100%

(ii) How would you get a non-statistician to describe their prior for this problem?

The expert has to allow for the dependence between the three probabilities. The easiest way for them to do this is would probably be to breakdown the prior into conditional stages. What proportion do you expect to be forested? What will be the proportion of grassland in the terrain that is not forested? Alternatively you could use a prior that is designed for probabilities that sum to one, such as a Dirichlet, and try to get the expert to understand that distribution. Perhaps you could generate some random data from Dirichlet distributions with different parameters and ask the expert to select the set that best reflects their opinion.