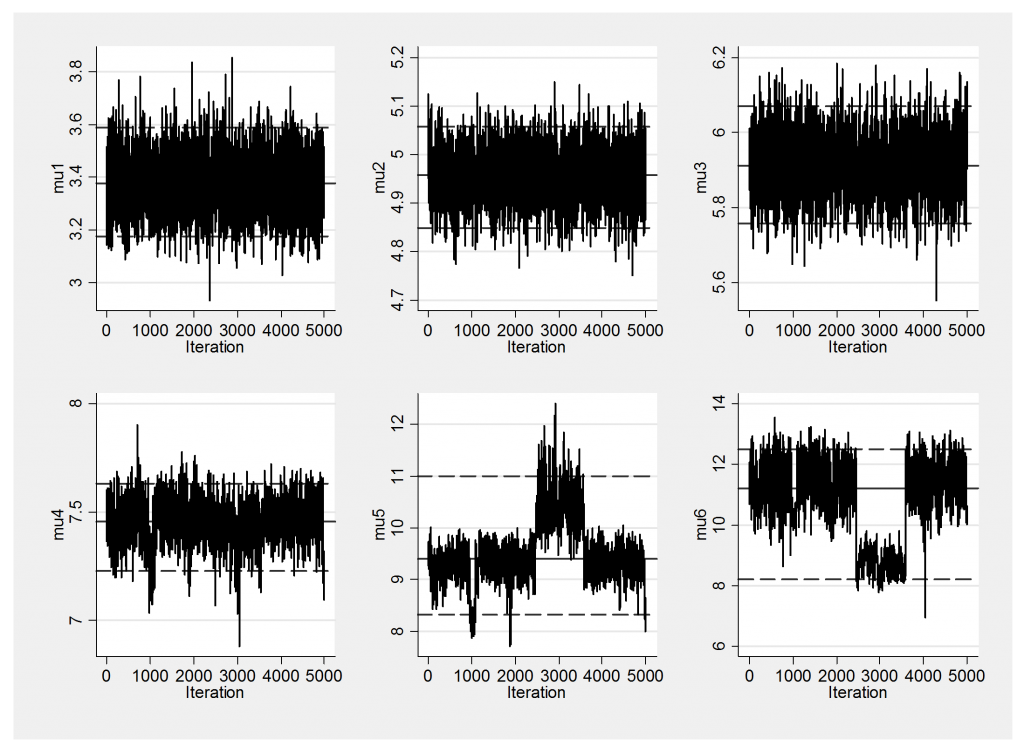
In my last posting (‘Mixtures of Normal Distributions’) I modelled a multi-modal distribution of fish lengths using a mixture of six normal distributions and noticed some label switching in the trace plots of the means of the components. Here is a repeat of the trace plot for the component means from a run of length 5,000.
Clearly mu5 and mu6 switch labels around iteration 3,000 so that the peak that was called number 5 becomes labelled as number 6 and vice versa. This is typical of a well-mixing chain and is not an indication of a problem with the algorithm. However, there is little sense in averaging mu5 or in looking at its marginal distribution because it partly captures one peak and partly another. The combined distribution of all of the components is unaffected by the label switching but the role of the individual parameters changes during the run.
Were this chain to be run for long enough, we would expect more of this type of switching affecting all six components, although of course a component that is well-separated from the others will switch labels much less frequently.
If, for some reason, we want to estimate the mean of the peak that is located close to 11 then we have a problem because part of that parameter’s distribution is stored as mu5 and part is stored as mu6.
There are essentially two approaches to avoid or compensate for the label switching:
- Use a prior that imposes a constraint that makes the components unique
- Run the algorithm with an unconstrained prior and then sort the simulations afterwards
The most important thing to realize is that if you sort the simulations afterwards by rearranging the labels, e.g. by relabeling the simulations that are close to 11 to always be called component 6, then effectively you are creating a solution under a different, more-constraining, prior. The drawback is that you will have created a solution under a prior that cannot easily be specified.
Some people can live with this type of ad hoc modification of the prior, but for me Bayesian analysis only makes sense if you really believe in the prior and you cannot say that you believe in a prior that you cannot specify. Consequently I am not a fan of relabeling algorithms.
The other option is to impose a constraint by changing the prior directly. Now we would be able to say exactly what was done and agree or otherwise with the choice. There may indeed be situations in which this makes sense. For example, with the fish data we might believe that each peak corresponds to fish born in a particular year, in which case we might be willing to assume that two year old fish will be larger than one year old fish. We might also believe that there will be more one year old fish than two year old fish or we might believe that fish only live for five years so there cannot be more than 5 genuine peaks. When such information exists there is, of course, no harm in using it, indeed it ought to be used, even though the priors may no longer be conjugate and we could lose the simplicity of the Gibbs sampler.
Often though, mixture models are used to represent non-normal distributions without there being sets of separate peaks corresponding to some previously known structure. Now it is not possible to define meaningful priors and our only option is to define a constraining prior based purely on convenience. For instance, we could insist that the mean of component 1 must be less than the mean of component 2 etc. But if we follow this route, why not use, the probability of component 1 must be more than the probability of component 2 etc.? It is possible that the component with the largest probability will have a mean of 3 at some iterations and a mean of 5 at other points in the chain. So sorting by one parameter may still allow switching of other parameters.
It is a natural instinct to try to give meaning to the components of a mixture after it has been fitted, but in my opinion it is an instinct that should be resisted. The model states that the distribution can be represented by a mixture and so it is the whole mixture distribution that is meaningful and not always the individual components. Except in special circumstances where we can place meaning on the components in advance of the model fitting, what we should be interested in are the properties of the mixture taken as a whole and not the properties of its components.
A particularly common example of over-interpretation of the individual components occurs when mixture models are used for cluster analysis and the components of the mixture are interpreted as if they represented separate clusters. Sometimes they do and sometimes they do not; cluster definition is a secondary issue that requires further analysis.
So what should we do about label switching? My solution is to do nothing to adapt the analysis, but instead to concentrate the interpretation on the full mixture distribution and not on its components. For an alternative view, there is a very good review by Jasra, Holmes and Stephens (Statistical Science 2005;20:50-67).


 Subscribe to John's posts
Subscribe to John's posts
John,
Thanks for a very interesting posting. I am a novice and still raw whenever label switching occurs. For example I have a binary negative binomial mixture:
p_Y(y|theta,loc,scale) = sum_{k=1}^K theta_k* NB2(loc,scale_k) and where loc=exp(x*beta)
Does label switching applies to such model when location is the same for all mixture components?
Can I deal with label switching by ordering theta, i.e. theta_1 < theta_2?
Thanks a lot, Linas
Linas, yes label switching will still apply to your mixture. You can tackle the problem by ordering the thetas as you suggest but whether or not this is the best thing to do will depend on the particular data set that you are analysing. My own feeling is that people over-interpret the components in mixture models and that it is often better to concentrate on the full mixture rather than its components.