Poisson regression with two random effects: WinBUGS, OpenBUGS and JAGS Options

In my last posting (available here) I described Stata programs that call WinBUGS, OpenBUGS or JAGS to fit a Poisson regression model with two random effects. WinBUGS, OpenBUGS and JAGS make automatic choices about the samplers that they use and in my previous comparison I accepted the defaults offered by those programs. This week I want to look at the options available in WinBUGS, OpenBUGS and JAGS to see if it is possible to improve their performance.

First let me recap the results that we obtained last time. The table below show the posterior means and their standard errors as obtained from the three programs when we made a run of length 50,000 thinned by taking every 5th value to leave 10,000 simulations. The standard errors reflect the sampling errors in the chain and are a measure of the quality of the mixing.

----------------------------------------------------------------------------
            WinBUGS       OpenBUGS      JAGS
 Parameter  mean  sem     mean  sem     mean  sem
 a0         1.595 0.0018  1.594 0.0014  1.596 0.0023
 aBase      0.911 0.0048  0.920 0.0029  0.892 0.0057
 aTrt      -0.802 0.0193 -0.780 0.0068 -0.856 0.0251
 aBXT       0.276 0.0139  0.262 0.0045  0.305 0.0179
 aAge       0.393 0.0069  0.398 0.0064  0.393 0.0084
 aV4       -0.098 0.0011 -0.100 0.0011 -0.100 0.0013
 sigmau     0.494 0.0006  0.495 0.0006  0.496 0.0006
 sigmae     0.407 0.0005  0.407 0.0005  0.406 0.0005
 ----------------------------------------------------------------------------

Remember that these results are stochastic so re-running any one of the programs with different starting values would give slightly different estimates, none the less a few things are evident.
(a) The standard errors are large for  aAge, aBase, aTrt and the interaction aBXT
(We saw previously that three of these estimates are highly correlated)
(b) JAGS has the largest sems, WinBUGS is slightly better, but OpenBUGS is a clear winner.

JAGS modules

JAGS is modularized to make it possible for the user to add extra components of their own to the basic program, although I suspect that this is rarely done because it is not straightforward. When JAGS is run in its default mode, two modules are automatically loaded; the base module and the bugs module, but the downloaded program provides four other modules,

mix: for fitting finite normal mixture distributions
dic: for calculating the deviance information criterion
msm: for fitting continuous-time multi-state models
glm: for block updating of generalized linear models

Clearly the glm module is specifically designed for handling problems such as our Poisson regression so to be fair to JAGS we need to see how it would perform with this module installed.

To make the loading of modules easier for the Stata user I have added a module option to wbsscript that only applies when creating scripts for JAGS. So to load the glm module we need to change the Stata command to,
wbsscript_v2 using script.txt, replace ///
    model(model.txt) data(data.txt) init(init.txt) log(log.txt) ///
    set(a0 aBase aTrt aBXT aAge aV4 tauu taue) ///
    burn(5000) update(50000) thin(5) coda(epi) jags module(glm)

At present this option is only available in the developmental ado file wbsscript_v2 that can be downloaded from my homepage. Eventually I will make it part of the next release of wbsscript. If we run this program (everything else is identical to the Stata code that we wrote last week) then we get results,

 -------------------------------------------------------------
 Parameter n   mean  sd    sem     median     5% CrI
 -------------------------------------------------------------
 a0     10000  1.594 0.081 0.0009  1.594 ( 1.435, 1.752 )
 aBase  10000  0.916 0.134 0.0014  0.918 ( 0.656, 1.173 )
 aTrt   10000 -0.782 0.384 0.0042 -0.784 ( -1.533, -0.022 )
 aBXT   10000  0.264 0.197 0.0021  0.265 ( -0.127, 0.645 )
 aAge   10000  0.399 0.341 0.0036  0.402 ( -0.266, 1.064 )
 aV4    10000 -0.098 0.092 0.0011 -0.098 ( -0.277, 0.085 )
 sigmau 10000  0.495 0.055 0.0006  0.491 ( 0.397, 0.612 )
 sigmae 10000  0.408 0.036 0.0006  0.407 ( 0.340, 0.483 )
 --------------------------------------------------------------

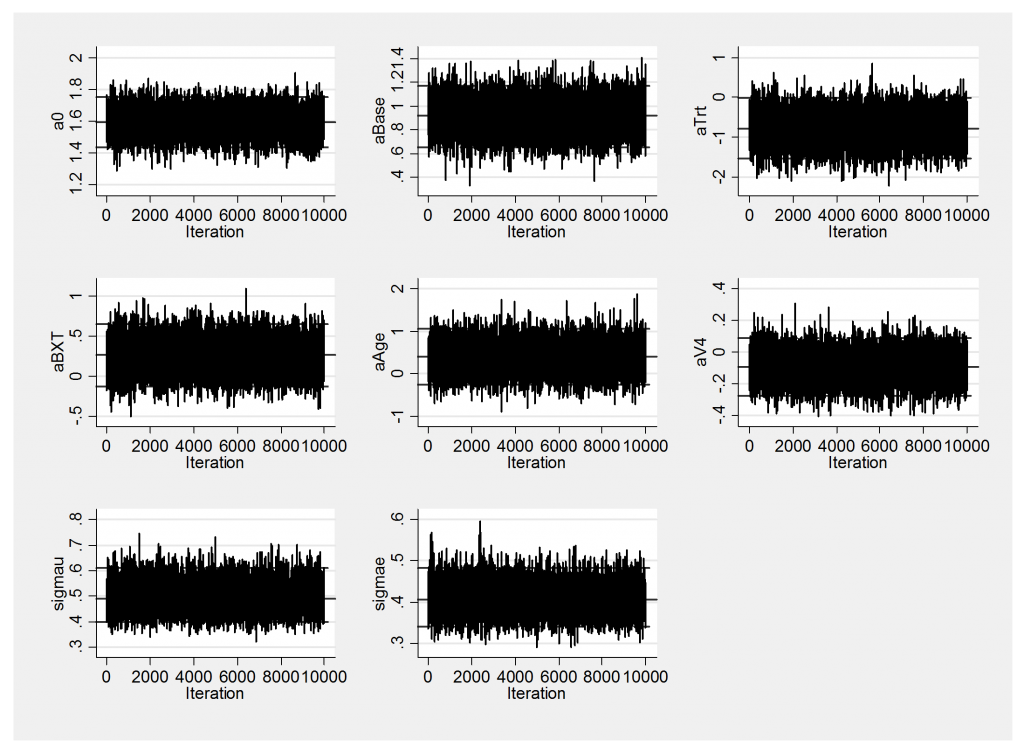
We have a new, clear winner! JAGS now out-performs OpenBUGS and is vastly better than WinBUGS. We can see the improved performance by comparing the trace plots with those obtained last week.

In fact the glm module is so good that we do not even need to centre the variables before fitting the model, although, if we decided not to centre, we would need to reassess our priors.

Over-relaxation

Like JAGS, both WinBUGS and OpenBUGS take automatic control of the choice of samplers. The choices are usually good but, because of this, WinBUGS and OpenBUGS lack flexibility. The one option that they do both offer is over-relaxation.

When running a sampler, there is usually a computational burden associated with the setting up of the algorithm followed by further computations to draw and test a single value. Often it would be little extra effort to draw ten values rather than one but standard MCMC only needs one value so this is not done. The idea of over-relaxation is to draw a set of values and then to choose one of them in such a way that we improve the mixing. There are various algorithms of making the selection but a popular one is to order the set of values together with the previous value. Then if the previous value is the largest, we choose the smallest as the next draw, if it is the second largest then we use the second smallest and so on. In this way an extreme value in one direction is followed by an extreme value in the other direction and so the mixing is improved.

There is an overrelax option for the Stata command wbsscript that, if set, asks WinBUGS or OpenBUGS to use over-relaxation. The result should be an algorithm that takes slightly longer to run but which mixes better.

When I set the overrelax option on the call to WinBUGS the analysis took 3.1 minutes compared with 2.25 minutes without over-relaxation. The results were,

 ----------------------------------------------------------------------------
Parameter         n     mean       sd      sem   median         95% CrI
----------------------------------------------------------------------------
 a0           10000    1.596    0.081   0.0012    1.596 (   1.437,   1.754 )
 aBase        10000    0.915    0.132   0.0039    0.914 (   0.658,   1.182 )
 aTrt         10000   -0.786    0.377   0.0151   -0.790 (  -1.531,  -0.049 )
 aBXT         10000    0.266    0.194   0.0116    0.266 (  -0.120,   0.645 )
 aAge         10000    0.392    0.349   0.0046    0.390 (  -0.297,   1.073 )
 aV4          10000   -0.099    0.092   0.0010   -0.098 (  -0.279,   0.082 )
 sigmau       10000    0.496    0.055   0.0006    0.493 (   0.397,   0.612 )
 sigmae       10000    0.407    0.036   0.0004    0.405 (   0.341,   0.481 )
----------------------------------------------------------------------------

The sem of aTrt has reduced from 0.0193 to 0.0151 equivalent to increasing the original run length from 50,000 to about 80,000 but the run time has increased from 2.25 minutes to 3.1 minutes so in that time we could have run 70,000 iterations. The gain is minimal and we would need to run several chains from different starting positions to establish that over-relaxation is a benefit at all.

With OpenBUGS the use of over-relaxation increased the run time from 1.5 minutes to 2.2 minutes and the results were,

----------------------------------------------------------------------------
Parameter         n     mean       sd      sem   median         95% CrI
----------------------------------------------------------------------------
 a0           10000    1.595    0.082   0.0013    1.596 (   1.431,   1.755 )
 aBase        10000    0.919    0.133   0.0026    0.917 (   0.657,   1.185 )
 aTrt         10000   -0.775    0.380   0.0062   -0.772 (  -1.527,  -0.038 )
 aBXT         10000    0.259    0.195   0.0042    0.257 (  -0.128,   0.642 )
 aAge         10000    0.394    0.349   0.0057    0.401 (  -0.297,   1.066 )
 aV4          10000   -0.098    0.092   0.0010   -0.099 (  -0.277,   0.082 )
 sigmau       10000    0.496    0.056   0.0006    0.493 (   0.397,   0.615 )
 sigmae       10000    0.407    0.036   0.0004    0.406 (   0.342,   0.482 )
----------------------------------------------------------------------------

The standard errors have hardly improved at all and it would definely have been better to have run the chain for longer without over-relaxation.

Conclusions

For this example, over-relaxation did not offer any benefit and we would have been at least as well off running the unrelaxed chain for longer. The improvement in JAGS from using the glm module was however dramatic and it turned JAGS from the slowest software into by far the quickest. Given the popularity of generalized linear mixed models this makes JAGS a sensible option, especially if it is being called from within Stata when we do not have to worry so much about reformatting the data or the initial values.

The more general message is perhaps that general purpose programs will always have their limitations and by using knowledge of the particular problem we can often design a better MCMC algorithm than WinBUGS, OpenBUGS or JAGS will provide. The balance is between the time taken to create such an algorithm and the time saved when the program is run. There are many people running WinBUGS for days at a time and perhaps they would benefit from standing back and thinking more about the problem. Not only might they find faster algorithms but the gain in speed might encourage them explore their models in a way that is not practical if every run takes days to complete.