This is a continuation my previous posting on non-parametric Bayesian analysis and this time I will try to show how a Dirichlet process can be used to create a family of distributions that provide much more flexible priors than the standard options such as the normal or gamma.
Last time we saw how we can represent a distribution over a finite number, J, of possible values by a set of probabilities, θj, j=1…J, and how we can create a prior for those probabilities by using a Dirichlet distribution, Dir(M,fj), with concentration parameter M and expected probabilities fj j=1…J.
Suppose now that we want to represent a distribution over an infinite number of points, i.e. a continuous distribution. We will have an infinite number of θj, j=1…∞ and the θ’s will describe probability densities rather than probabilities. The generalization of the Dirichlet distribution will have a concentration parameter M and an infinite set of expected probability densities. The expected densities together define a distribution F, which is usually called the base distribution, and the family of distributions is defined by the Dirichlet process DP(M,F).
Our main problem in using this approach is that we do not have a simple algorithm for generating a random distribution, say f(), from the family of possibilities defined by the Dirichlet process DP(M,F), but what we do have is the Chinese restaurant algorithm that was introduced in my previous posting. This tells us how to generate a random sample X1…Xn from a random f() drawn from DP(M,F). In the infinite form the Chinese restaurant algorithm says
For i=1…n
With probability M/(M+i-1)
draw Xi from the expected distribution F
Otherwise
select a random integer j between 1 and i-1 and set Xi = Xj
What we could do, of course, is to generate a large sample using this algorithm and then look at the histogram to discover what f() looks like.
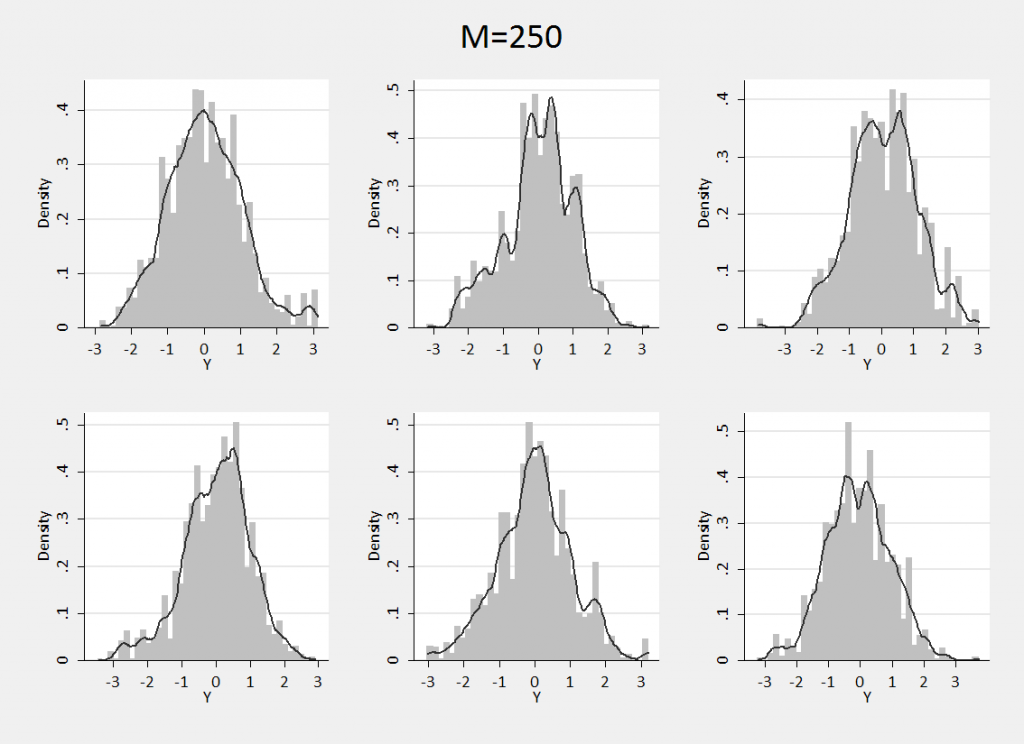
To illustrate this process I assumed that my base distribution was N(0,1) and that I was confident that the actual distribution was not a long way from the base distribution, so I choose a very large concentration parameter M=250. Then I drew six different samples each of size 5000 using the Chinese restaurant algorithm and plotted their histograms with an overlayed smooth density. The Stata command for such plots is,
. histogram X, xlabel(-3(1)3) kdensity color(gs12)
Combining the six plots gives,
We can see that the family of distributions defined by this Dirichlet process quite closely resembles a standard normal but can have small extra bumps or thicker tails. If we use this prior, our belief is that the distribution will be drawn from the family of possibilities illustrated by these six examples.
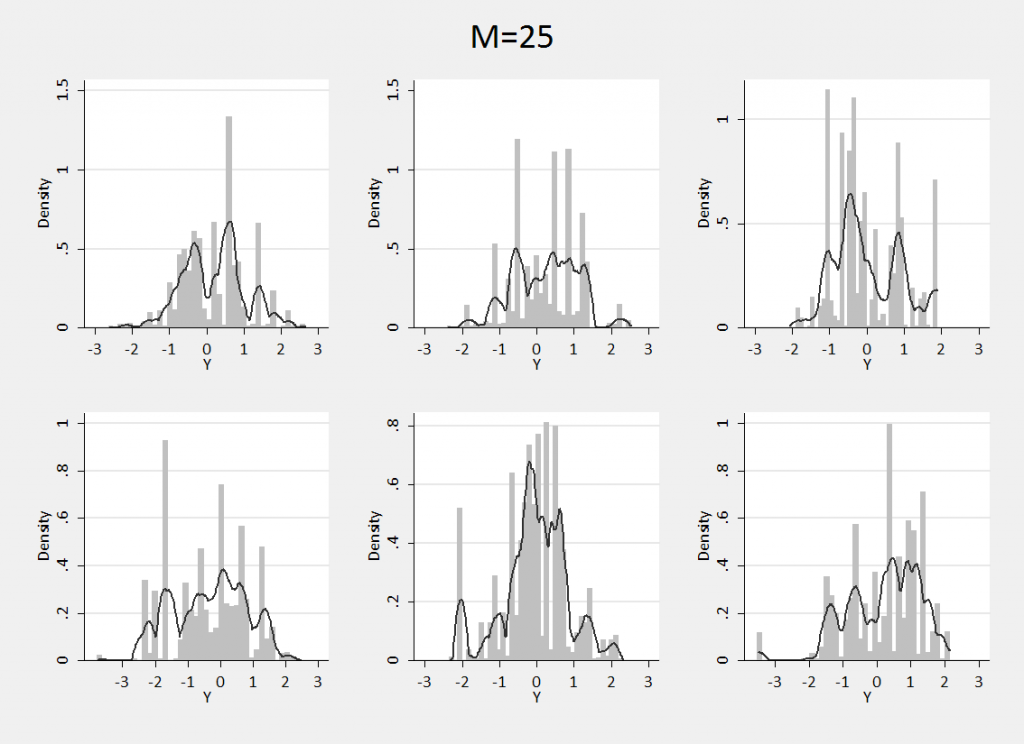
Repeating the process with M=25 we can see what happens if we specify a prior that is much freer to diverge from the base distribution.
We have almost lost the normal shape entirely although the distributions are still concentrated over the same range of values. In this case our prior belief is that the distribution could be very multimodal and we are claiming to know very little about the shape.
Learning from real data
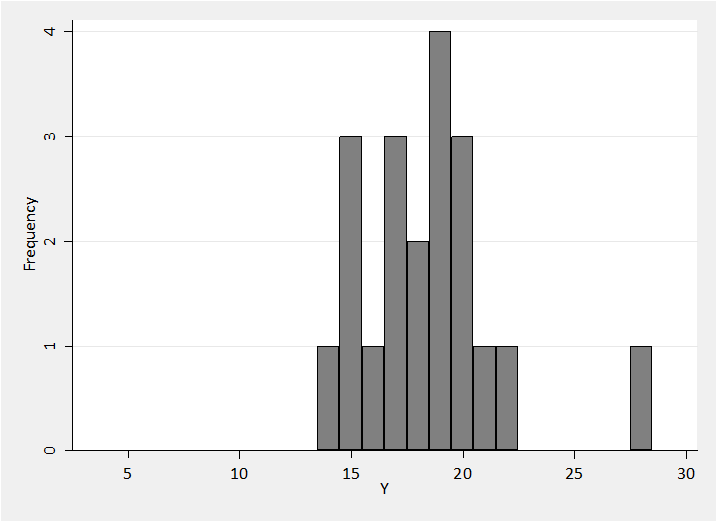
Let’s see how this works in practice. Suppose that an ophthalmologist brings you a set of measurements of the pressure (IOP) in the right eyes of a sample of 20 patients. The readings in units of mm Hg are shown in the histogram below.
The ophthalmologist tells you that several large surveys have shown that IOP is approximately normally distributed over the general population with a mean of 17 and a standard deviation of 3. The aim is to estimate the distribution of IOP in this patient group.
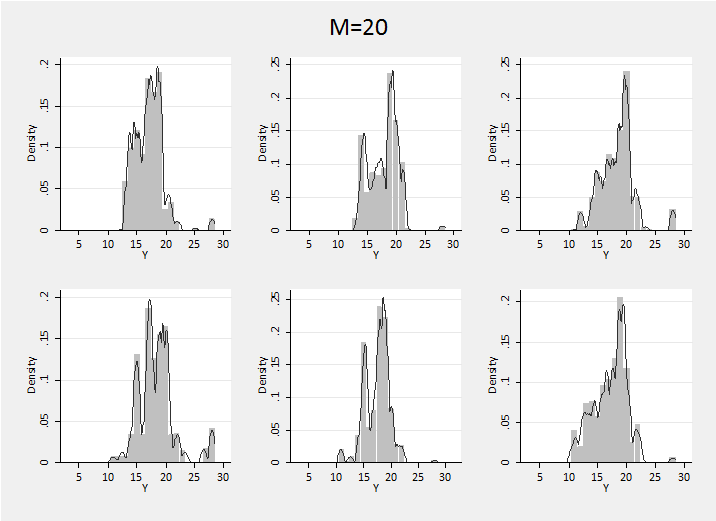
We will use the N(17,3) distribution as our base function in a Dirichlet process and make the concentration parameter equal to 20. This is the same as the sample size so we are weighting the prior and data more or less equally. We know that a prior with M=20 is very spikey and with only 20 data values we can anticipate a very spikey posterior.
To picture the posterior of the family of distributions I ran the Chinese Restaurant algorithm to create a sample of 10,000 values starting with the 20 real observations and then adding 21…10,000 according to the algorithm.
The posterior distributions are quite variable and illustrate how the clustering of values inherent in the Dirichlet process can randomly lead to any one of the data’s peaks becoming dominant. We have little information and are forced to conclude that the distribution of IOP in the patient population might look like any one of these examples.
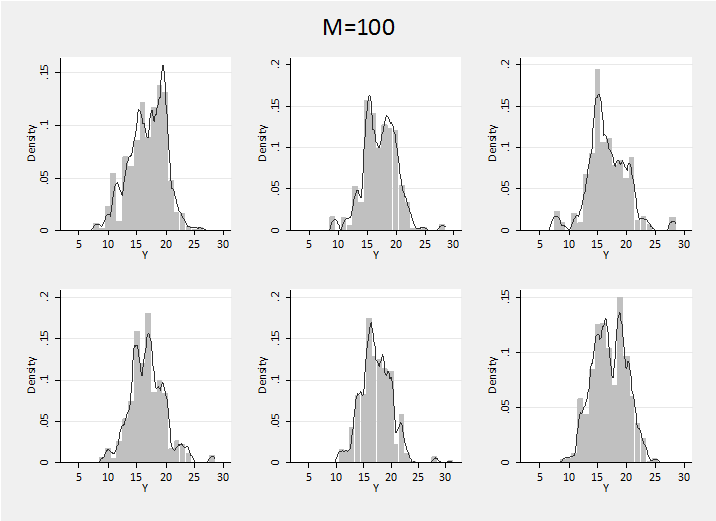
These distributions are spikier that I find credible for IOP, so perhaps I really believe in a larger M. Here is a sample of distributions generated with M=100
Of course we get a less variable posterior that is closer to N(17,3).
In fact I would like to be even more certain that the shape is close to normal, but less certain of the values 17 and 3. This can be done by placing higher level priors on the mean and precision of the base distribution. For instance, we could say that the base distribution is F=N(mu,tau) with mu~N(17,0.5) and tau~G(10,1/90) (mean tau=1/9 corresponding to a standardard deviation of 3).
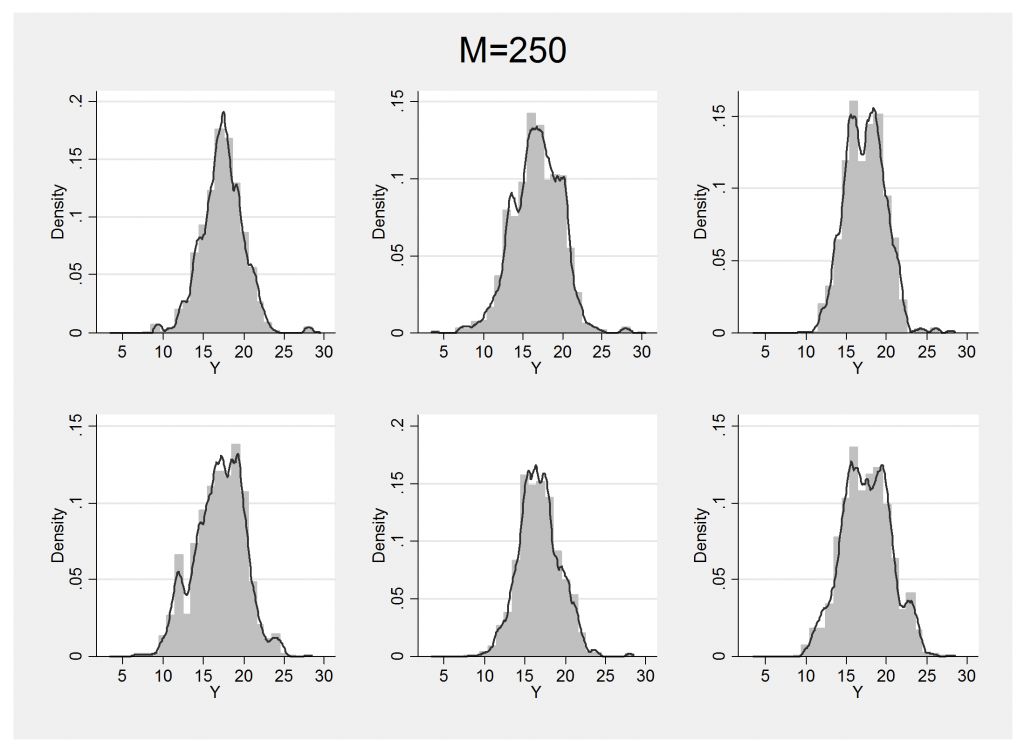
Now to generate the examples we simply draw random values from the priors on mu and tau then use those values to define the base distribution for the Dirichlet process. Choosing a strong concentration parameter, M=250, to ensure that we do not get too non-normal, the uncertainty in the posterior is illustrated by the six examples below. As we would expect, the shape deviates less from normality but the mean and standard deviation change.
Next time I will show how a Dirichlet process can use as one of the priors in a Bayesian model and how all of the posterior parameter estimates can be updated in a MCMC algorithm.


 Subscribe to John's posts
Subscribe to John's posts
Recent Comments