In Leicester we run a masters course in Medical Statistics and each year our students get a two-day course on fitting models by maximum likelihood using Stata’s -ml- command. For the last few years I have taught this course and so I have been on the lookout for examples based on real data that I can use as exercises for the students or as coursework for assessment.
This year I based the assessment on the analysis of the correlation between two measurements of viral load made on women with HIV. These data would also make a good example to illustrate Gibbs sampling in Stata and so over a couple of postings I will present a Bayesian analysis of these data and discuss a few issues that it raises.
First let me describe the problem. Viral load is a measurement of the severity of a viral infection. It involves taking a sample of a body fluid, often blood plasma, and seeing how much viral RNA can be detected in the sample, the units of measurement are therefore, RNA copies per millilitre. The main complication for the statistician is that the assay has a lower limit of detection, so when the amount of viral RNA in the blood is very low, it will not be detected.
In this particular study, women with an HIV infection had their viral loads measured in both blood and saliva samples and the objective of our analysis is to estimate the correlation between the two measurements. The women had been on antiretroviral therapy and as a result many of them had undetectable levels of the virus.
Priors
If we are to make a Bayesian analysis then prior knowledge is important, so to help us develop our priors, here is a scatter plot of the results from a different, but similar, study (Shepard et al. J Clin Microbiol 2000;38:1414-1417)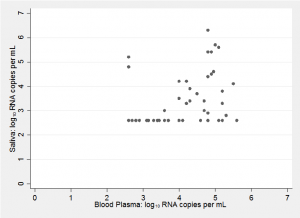
The assay used in Shepard’s study had a lower limit of detection of 400 HIV viral RNA copies per mL. So, on a log10 scale there are no values below 2.6 and in my plot subjects with measurements below the limit of detection are shown at 2.6.
There are several aspects of this plot that might influence ours priors;
- The standard method of modelling log10 viral loads is to use a normal distribution. This is not obviously wrong, but it is difficult to justify the model when the number of samples is small and so many readings are below the level of detection.
- The amount of viral RNA in saliva is much lower than that in blood plasma with far more readings below the level of detection. The authors commented in their discussion that viral loads in non-blood samples tended to be 1 or 2 units lower on a log10 scale.
- Few people have log10 measurements over 6, that is, viral loads over a million.
- The correlation is positive but not strong and the assay seems to throw up the occasional outlier.
- The paper by Shepard et al. makes frequent reference to the differences between measurements made with different assays and even to differences between different laboratories using the same assay.
The data
The data for our analysis come from the Women’s Interagency HIV Study (Barkan et al Epidemiology 1998;9:117-125) from which 195 women, who had been on antiretroviral therapy, were selected to have their viral load measured in both plasma and saliva samples. The objective is to estimate the correlation between the two viral loads. Some women had viral loads below the limit of detection, which for this particular assay was 80 RNA copies per mL.
The model
These data were used to illustrate a maximum likelihood analysis of a mixture model (Chu et al Applied Statistics 2005;54:831-845). The data are available at http://onlinelibrary.wiley.com/journal/10.1111/(ISSN)1467-9876/homepage/series_c_datasets.htm . My students were required to use a model based on a single bivariate normal distribution, an analysis that closely follows an earlier approach (Lyles et al Biometrics 2001;57:1238-1244).
The Bayesian model that we will use will also follow Lyles et al. and so will be based on a bivariate normal distribution and the main issue will be how to handle the censored values that fall below the limit of detection. I will analyse the data in my next posting but I will finish today by making a few comments about the maximum likelihood exercise that I set for the students.
The student exercise
If you are interested you can download the questions for the maximum likelihood analysis from here, ViralLoadCoursework. When I set the coursework I thought that is was a reasonable challenge but in fact most students got very high marks so perhaps it was easier than I thought.
The format that I use for student coursework is fairly constant. I encourage them to have informal priors to guide their interpretation, so even when the analysis is not Bayesian, I always start by getting the students to read about the medical background to the problem. However, students find it quite difficult to judge how much of the biology/medicine they need to know. So I try to give them some guidance, hopefully without being too constraining.
Obviously the exercise is graded so that the tasks become more difficult as the students progress. I do not expect every student to complete every task so I give them a guide as to how much time they should spend on the whole exercise and I tell them, in reasonable detail, what marking scheme I will use. I am sure that students actually spend longer on my coursework than I suggest, but a target is useful in getting them to think about time management.
The other point that I wanted to mention is the difficulty that I find in getting students to generalize from the specific analysis before them. Let me take one particular task as an illustration. When a measure of viral load in a single fluid is censored at the lower level of detection then those missing values need to be estimated and this can induce a correlation between the estimates of the mean and standard deviation of the normal distribution. It is simple to get -ml- to display the estimate of this correlation and most students will happily find this value, although I suspect that some remain confused by correlations between estimates and correlations between measurements.
The point here though is my concern to get them to think beyond the specific example and to answer questions such as,
• Will the correlation always be positive or always negative or will it vary?
• How is the size of the correlation related to the amount of censoring?
I think that students find such questions difficult because they require a good mental picture of what is happening in the analysis. When they cannot see the answer immediately, they are encouraged to investigate by simulation and, hopefully, in the process they will develop their mental picture of the analysis.
In my next posting I will concentrate on the Bayesian analysis of this problem using a Gibbs sampler programmed in Stata.


 Subscribe to John's posts
Subscribe to John's posts
Recent Comments